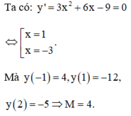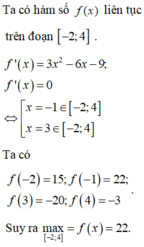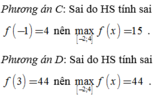tìm giá trị lớn nhất của biểu thức B=3x2+9x+1 phần 3x2+9x+7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
24 tháng 10 2017
B = 9 x - 3 x 2 = 3 3 x - x 2 = 3 9 / 4 - 9 / 4 + 2 . 3 / 2 x - x 2
= 3 9 / 4 - 9 / 4 - 3 / 2 x + x 2
= 3 9 / 4 - 3 / 2 x - x 2 = 27 / 4 - 3 / 2 - x 2
Vì 3 / 2 - x 2 ≥ 0 với mọi x
⇒ B = 27/4 − 3 / 2 - x 2 ≤ 27/4 do đó giá trị lớn nhất của B bằng 27/4 tại x = 3/2
CM
3 tháng 7 2017
Đáp án D
Ta có: y ' = 3 x 2 + 6 x − 9 ⇒ y ' = 0 ⇔ x = 1 x = − 3
Vậy GTLN của hàm số đã cho trên − 2 ; 2 là:
max − 2 ; 2 y = max y − 2 ; y 1 ; y 2 = max 29 ; 2 ; 9 = 29
CM
23 tháng 2 2018
Đáp án A
Ta có y ' = 3 x 2 − 6 x + m .Hàm số có cực trị ⇔ P T y ' = 0 có nghiệm phân biệt ⇔ Δ ' y ' > 0 ⇔ 9 − 3 m < 0 ⇔ m < 3.
CM
24 tháng 3 2019
Đáp án D
Ta có: y ' = 3 x 2 + 6 x − 9 ; y ' = 0 ⇔ x = 1 x = − 3 l .
Ta có y − 1 = 4 ; y 1 = − 12 ; y 2 = − 5
Do đó giá trị lớn nhất của hàm số là M = 4
CM
12 tháng 5 2018
Chọn C
TXĐ: D = ℝ , suy ra hàm số đã cho liên tục trên đoạn [-2;2].
PT
1
CM
19 tháng 2 2017
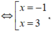
- Thay x = 1 vào biểu thức 3x2 – 9x, ta có:
3.12-9.1 = 3.1 - 9 = 3 - 9 = -6
Vậy giá trị của biểu thức 3x2 – 9x tại x = 1 là – 6
- Thay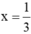 
vào biểu thức trên, ta có:
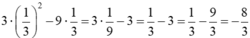
Vậy giá trị của biểu thức 3x2 – 9x tại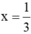 
là 
NA
3
2 tháng 3 2022
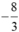
\(3x^2-9x=3x\left(x-3\right)\)
Thế x=1 ta được:
\(3.1\left(1-3\right)=3.-2=-6\)
Thế x=\(\dfrac{1}{3}\) ta được:
\(3.\dfrac{1}{3}\left(\dfrac{1}{3}-3\right)=1-\dfrac{8}{3}=-\dfrac{8}{3}\)
