Mọi người giải chi tiết hộ em ạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
0
21 tháng 10 2021
\(B=-x^2+2x-4\)
\(=-\left(x^2-2x+4\right)\)
\(=-\left(x-1\right)^2-3\le-3\forall x\)
Dấu '=' xảy ra khi x=-3
LT
0
M
2
H
4 tháng 4 2021
Gọi số sản phẩm dự định là a (sản phẩm ) (a là số tự nhiên khác 0)
Vì theo dự định mỗi ngày sản xuất 50 sản phẩm nên số ngày theo dự định là \(\dfrac{a}{50}\)
Nhưng thực tế , đội đã sản xuất theeo được 30 sản phẩm do mỗi ngày vượt mức 10 sản phẩm (nghĩa là sản xuất 60 sản phẩm) , nên số ngày thực tế là \(\dfrac{a+30}{60}\)
Vì thực tế sớm hơn dự định 2 ngày nên ta có phương trình :
\(\dfrac{a}{50}=\dfrac{a+30}{60}+2\\ \Leftrightarrow6a=5\left(a+30+120\right)\\\Leftrightarrow a=750\left(t.m\right) \)
Vậy số sản phẩm dự định là 750 sản phẩm
4 tháng 4 2021
Bài 3:
Gọi số sản phẩm đội phải sản xuất theo kế hoạch là x( sản phẩm, x\(\in N\)*)
Thời gian đội sản xuất theo kế hoạch là: \(\dfrac{x}{50}\) (ngày)
Số ngày làm thực tế là: \(\dfrac{x+30}{50+10}=\dfrac{x+30}{60}\) (ngày)
Theo bài ra, ta có phương trình:
\(\dfrac{x}{50}-\dfrac{x+30}{60}=2\)
\(\Leftrightarrow\dfrac{60x-50\left(x+30\right)}{50.60}=2\)
\(\Leftrightarrow60x-50x-1500=6000\Leftrightarrow x=750\)(thoả mãn)
Vậy theo kế hoạch đội phải sản xuất 750 sản phẩm
NM
0
11 tháng 3 2022
theo mình thì câu trên: dưới mẫu trong căn bỏ n^2 ra làm nhân tử chung xong đặt nhân tử chung của cả mẫu là n^2 . câu dưới thì mình k biết!!
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
\(\lim\dfrac{-3n+2}{n-\sqrt{4n+n^2}}=\lim\dfrac{\left(-3n+2\right)\left(n+\sqrt{4n+n^2}\right)}{\left(n-\sqrt{4n+n^2}\right)\left(n+\sqrt{4n+n^2}\right)}\)
\(=\lim\dfrac{\left(-3n+2\right)\left(n+\sqrt{4n+n^2}\right)}{-4n}=\lim\dfrac{n\left(-3+\dfrac{2}{n}\right)n\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4n}\)
\(=\lim n\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}\)
Do \(\lim\left(n\right)=+\infty\)
\(\lim\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}=\dfrac{\left(-3+0\right)\left(1+\sqrt{0+1}\right)}{-4}=\dfrac{3}{2}>0\)
\(\Rightarrow\lim n\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}=+\infty\)
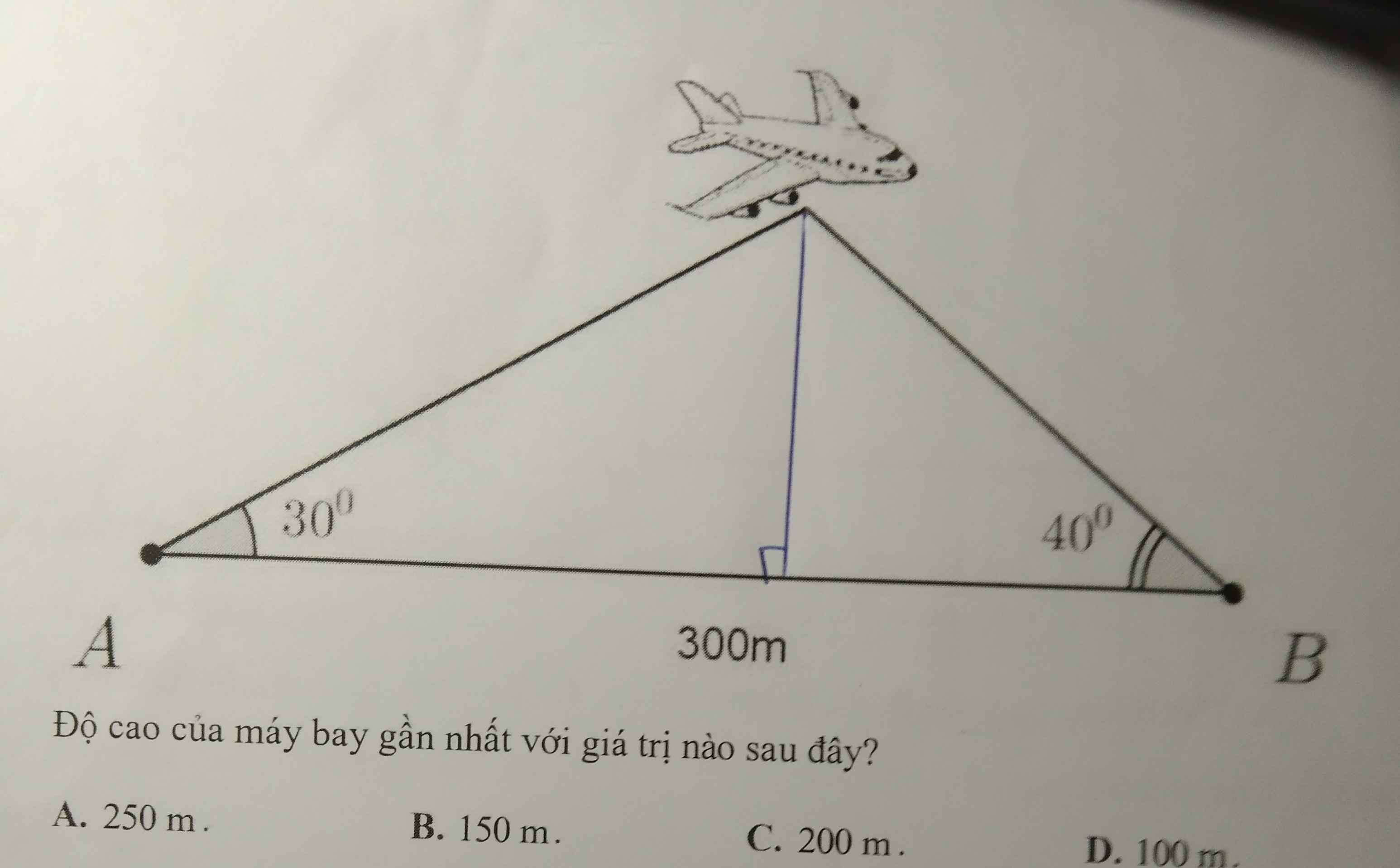
Cứu em với, giải đầy đủ xíu. theo PTHH đó e
hệ số của Fe2O3 là 1
hệ số của H2 là 3
->n H2=3n Fe2O3
dùng tỉ lệ của hệ số
VD: Tỉ lệ hệ số của Fe2O3 và H2 là 1/3
=> Tỉ lẹ số mol = 1/3 => nFe2O3 = 1/3nH2
=> nH2 = 0,1 : 1/3 = 0,3 (mol)