cho hàm số y=ax2
a) xác định hệ số a biết đồ thị (P) của nó đi qua A(4;4)
b) viết phương trình đường thẳng (d) đi qua A và tiếp xúc với (P)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 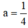
Vậy hàm số: 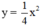
| x | -4 | -2 | 0 | 2 | 4 |
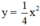 |
4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số:
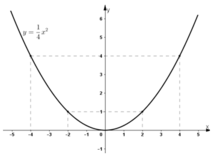

Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 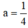
Vậy hàm số: 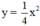
| x | -4 | -2 | 0 | 2 | 4 |
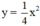 |
4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số:
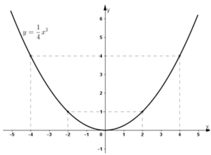

Lời giải:
a) Vì ĐTHS đi qua điểm $A$ nên:
$y_A=ax_A^2$
$\Leftrightarrow -1=a.2^2\Rightarrow a=-\frac{1}{4}$
b) Vậy hàm số có công thức: $y=\frac{-1}{4}x^2$
Hình vẽ:

a, y = ax^2 đi qua B(2;4)
<=> 4a = 4 <=> a = 1
b, bạn tự vẽ
a: Thay x=2 và y=4 vào hàm số, ta được:
\(a\cdot4=4\)
hay a=1
b: Thay x=2 và y=4 vào hàm số, ta được:
4a=4
hay a=1

dễ mà tự giải đi bạn ưi tui ko bít cách giải đâu nên đừn hỏi
a) đồ thi của hàm số đi qua A ( 4;4 ) nên x = y = 4
Thay vào hàm số y = ax2,ta có :
4 = 42 . a\(\Rightarrow\)a = 0,25
b) gọi đường thẳng ( d ) là : y = bx + c
vì ( d ) đi qua A nên 4 = 4b + c
Xét phương trình hoành độ giao điểm, ta có : 0,25x2 = bx + c
\(\Rightarrow x^2=\frac{bx+c}{0,25}=4bx+4c\)
\(\Leftrightarrow x^2-4bx-4c=0\)
\(\Leftrightarrow x^2-4bx-4\left(4-4b\right)=0\)
\(\Leftrightarrow x^2-4bx+16b-16=0\)
( d ) tiếp xúc với ( P ) nên : \(\Delta=\left(4b\right)^2-4\left(16b-16\right)=0\)
\(=16b^2-64b+64=\left(4b-8\right)^2=0\)
\(\Leftrightarrow b=2\)
suy ra c= -4
vậy pt đường thẳng ( d ) là y = 2x - 4