Rút gọn biểu thức sau.
-10 + (x - 16) + 9=−10+(x−16)+9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
1
27 tháng 1 2022
\(B=\dfrac{2^{15}\cdot5^8-2^5\cdot2^9\cdot5^9}{2^{16}\cdot5^7+2^{16}\cdot5^8}=\dfrac{2^{14}\cdot5^8\cdot\left(2-5\right)}{2^{16}\cdot5^7\left(1+5\right)}=\dfrac{1}{4}\cdot5\cdot\dfrac{-1}{2}=\dfrac{-5}{8}\)
CX
0
25 tháng 4 2021
\(a,B=4\sqrt{x=1}-3\sqrt{x+1}+2\)\(\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
\(b,\)đưa về \(\sqrt{x+1}=4\Rightarrow x=15\)
29 tháng 4 2021
a, Với \(x\ge-1\)
\(\Rightarrow B=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
b, Ta có B = 16 hay
\(4\sqrt{x+1}=16\Leftrightarrow\sqrt{x+1}=4\)bình phương 2 vế ta được
\(\Leftrightarrow x+1=16\Leftrightarrow x=15\)
CM
11 tháng 6 2019
a) Rút gọn:
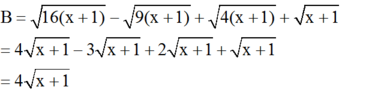
b) Để B = 16 thì:
⇔ x + 1 = 16 ⇔ x = 15 (thỏa mãn x ≥ -1)
8 tháng 7 2021
a.
\(B=\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}\left(x\ge-1\right)\)
\(B=\sqrt{16}.\sqrt{x+1}-\sqrt{9}.\sqrt{x+1}+\sqrt{4}.\sqrt{x+1}+\sqrt{x+1}\)
\(B=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)
\(B=\left(4-3+2+1\right).\sqrt{x+1}\)
\(B=4.\sqrt{x+1}\)
b.
\(B=16\\\)
\(\Rightarrow4\sqrt{x+1}=16\)
\(\Rightarrow\sqrt{x+1}=\dfrac{16}{4}=4\)
\(\Rightarrow x+1=4^2\)
\(\Rightarrow x+1=16\rightarrow x=16-1=15\) (thỏa mãn)
vậy x=15
1 tháng 1 2022
a: Thay x=16 vào A, ta được:
\(A=\dfrac{2\cdot4}{4+3}=\dfrac{8}{7}\)
TH
7 tháng 9 2017
a, \(=\frac{8\left(x+2y\right)^5}{2\left(x+2y\right)}=8\left(x+2y\right)^4\)
b,\(=\left(\frac{3}{4}\right)^{45}:\left(\left(\frac{3}{4}\right)^2\right)^{10}\)
\(=\left(\frac{3}{4}\right)^{45}:\left(\frac{3}{4}\right)^{2.10}=\left(\frac{3}{4}\right)^{25}\)
-10 + (x - 16) + 9=−10+(x−16)+9
-10 + x - 16 + 9 = -10 + x - 16 +9
\(\Rightarrow\)-10 + x -16 = -10 + x -16
\(\Rightarrow\)-10 + x = -10 +x
\(\Rightarrow\)x - 10 = x - 10
\(\Rightarrow\)x = x
có ai kết bạn với mình không???????