Một người muốn làm một chiếc quạt có chu vi là 80cm . Tìm số đo của góc AOB sao cho diện tích của chiếc quạt lớn nhất .
\(\frac{4x}{4x^2-8x+7}+\frac{3x}{4x^2-10x+7}=1\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TL
0
NM
1
12 tháng 4 2019
Xét \(x=0\)không thỏa mãn pt
Chia cả tử và mẫu của 2 phân số cho x ta được :
\(\frac{4}{4x-8+\frac{7}{x}}+\frac{3}{4x-10+\frac{7}{x}}=1\)
Đặt \(4x+\frac{7}{x}-9=a\)
\(pt\Leftrightarrow\frac{4}{a+1}+\frac{3}{a-1}=1\)
\(\Leftrightarrow\frac{4\left(a-1\right)+3\left(a+1\right)}{\left(a+1\right)\left(a-1\right)}=1\)
\(\Leftrightarrow4a-4+3a+3=\left(a-1\right)\left(a+1\right)\)
\(\Leftrightarrow7a-1=a^2-1\)
\(\Leftrightarrow a^2-1-7a+1=0\)
\(\Leftrightarrow a\left(a-7\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}a=0\\a=7\end{cases}}\)
Thay a vào tiếp tục giải pt là xong
HT
0
ND
1
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2019
ĐKXĐ: \(x\ne0\)
\(\Leftrightarrow\frac{4x}{4x^2-8x+7}+\frac{3x}{4x^2-10x+7}=1\)
\(\Leftrightarrow\frac{4}{4x-8+\frac{7}{x}}+\frac{3}{4x-10+\frac{7}{x}}=1\)
Đặt \(4x-8+\frac{7}{x}=a\) phương trình trở thành:
\(\frac{4}{a}+\frac{3}{a-2}=1\) \(\Leftrightarrow a\left(a-2\right)=4\left(a-2\right)+3a\)
\(\Leftrightarrow a^2-9a+8=0\Rightarrow\left[{}\begin{matrix}a=1\\a=8\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-8+\frac{7}{x}=1\\4x-8+\frac{7}{x}=8\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}4x^2-9x+7=0\left(vn\right)\\4x^2-16x+7=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{1}{2}\\x=\frac{7}{2}\end{matrix}\right.\)
9 tháng 8 2017
PP chung ở cả 3 câu,nói ngắn gọn nhé:
Chứng mình x khác 0,hay nói cách khác x=0 không là nghiệm của phương trình.
Chia cả tử và mẫu cho x ,rồi giải bình thường bằng cách đặt ẩn phụ.
Vd ở câu a>>>4/(4x-8+7/x)+3/(4x-10+7/x)=1.Sau đó đặt 4x+7/x=a>>>4/(a-8)+3/(a-10)=1>>>giải bình thường,các câu sau tương tự
ND
5
NH
1 tháng 2 2019
\(4x^2+4x+10=\left(2x+1\right)^2+9\)
Ma \(\left(2x+1\right)^2\ge0\Rightarrow\left(2x+1\right)^2+9\ge9\)
\(\Rightarrow\frac{3}{4x^2+4x+10}\le\frac{3}{9}=\frac{1}{3}\)
(dau "=" xay ra khi x=\(\frac{-1}{2}\)
CM
11 tháng 2 2019
Đáp án A
Phương pháp giải:
Tìm giá trị lớn nhất của thể tích khối nón và áp dụng công thức tính độ dài cùng tròn
Lời giải:
Gọi r, h lần lượt là bán kính đáy, chiều cao của phễu hình nón.
Thể tích của khối nón là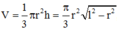 
với l là độ dài đường sinh và l = R bán kính tấm bìa hình tròn => 
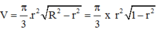vì chuẩn hóa R = 1
Xét hàm số 
trên (0;1) có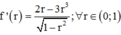 
Ta có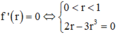 
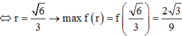
Do đó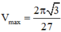 
Dấu “=” xảy ra khi và chỉ khi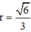 
Mà độ dài cung phần cuộn làm phễu chính là chu vi đáy hình nón
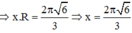
\(\frac{4x}{4x^2-8x+7}+\frac{3x}{4x^2-10x+7}=1\)
\(\Leftrightarrow4x\left(4x^2-10x+7\right)+3x\left(4x^2-8x+7\right)=\left(4x^2-8x+7\right)\left(4x^2-10x+7\right)\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=5\end{cases}}\)
Bài 1 :
Gọi x là bán kính quạt, y là độ dài cung tròn
Ta có chu vi quạt là 2x+y=80
Ta có công thức tính diện tích hình quạt:
\(S=\frac{\pi x^2\alpha}{360}\) và độ dài cung tròn:\(y=\frac{2\pi x\alpha}{360}\)
Ta có: \(\frac{2\pi xa}{360}+2x=80\)
\(\Leftrightarrow\alpha=\frac{14400-360x}{2\pi x}\)
\(\Rightarrow S=\frac{\pi x^2a}{360}=\frac{\pi.x^2.\frac{14400-360x}{2\pi x}}{360}\)
\(=\frac{\left(40-x\right)x}{2}=\frac{-x^2+40x}{2}=\frac{-\left(x^2-40x+400\right)}{2}+200\)
\(=\frac{-\left(x-20\right)^2}{2}+200\)
Vì \(\frac{-\left(x-20\right)^2}{2}\le0\forall x\)
=> \(S\le200\forall x\)
Dấu = xảy ra khi và chỉ khi x=20
\(\Rightarrow\alpha=\frac{180}{\pi}\)