Cho tam giác ABC cân tại A có AB =AC=34 cm , BC= 32 cm. Kẻ đường
trung tuyến AM .
a) Chứng minh AM vuông góc với BC .
b) Tính độ dài AM .
c) Tinh chu vi và diện tích tam giác AMB .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 4 2022
Cho tam giác ABC cân ở A, đường trung tuyến AM.
a) Chứng minh AM BC
b) Tính AM biết rằng AB cm BC cm 10 , 12
17 tháng 3 2018
a/Ta có: ΔABC cân ở A(gt)
mà AM là đường trung tuyến, nên AM cũng là đường cao
Vậy AM ⊥ BC
b/ Vì M là trung điểm của BC
nên BM=BC:2=32:2=16 (cm)
Xét ΔABM vuông tại M có:
AB2=AM2+BM2 (Định lý Py-ta-go)
nên 342=AM2+162
1156=AM2+256
AM2=1156-256
AM2=900
Vậy AM=30 (cm)
26 tháng 3 2018
a. Xét ΔAMB và ΔAMC, ta có:
AM = AC (gt)
BM = CM (gt)
AM cạnh chung
Suy ra: ΔAMB = ΔAMC (c.c.c)
Suy ra: ∠(AMB) = ∠(AMC) (1)
Lại có: ∠(AMB) + ∠(AMC) = 180o (hai góc kề bù) (2)
Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90o
Vậy AM ⊥ BC.
b. Tam giác AMB có ∠(AMB) = 90o
Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:
AB2 = AM2 + BM2 ⇒ AM2 = AB2 - BM2 = 342 - 162
= 1156 - 256 = 900
Suy ra: AM = 30 (cm).
10 tháng 3 2022
1: Xét ΔAMB và ΔAMC có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó:ΔAMB=ΔAMC
2:
a: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-50^0}{2}=65^0\)
b: BC=6cm nên BM=3cm
=>AB=AC=5cm
3: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF
hay ΔAEF cân tại A
20 tháng 3 2020
a) Xét tam giác AMB và AMC có:
AM chung
AB=AC (tam giác ABC cân tại A)
\(\widehat{A_1}=\widehat{A_2}\)(AM là phân giác)
=> \(\Delta AMB=\Delta AMC\left(cgc\right)\)(đpcm)
b) Có tam giác ABC cân tại A (gt); AM là trung tuyến tam giác ABC
Vì trong tam giác cân đường trung tuyến trùng với đường cao
=> AM là đường cao tam giác ABC
=> AM _|_ BC (đpcm)
20 tháng 3 2020
Bài làm
a) Xét tam giác AMB và tam giác AMC có:
^MAB = ^MAC ( Do AM phân giác )
AB = AC ( Do ∆ABC cân )
^B = ^C ( Do ∆ABC cân )
=> ∆AMB = ∆AMC ( g.c.g )
b) Cách 1: Vì ∆AMB = ∆AMC ( cmt )
=> ^AMB = ^AMC
Mà ^AMB + ^AMC = 180° ( hai góc kề bù )
=> ^AMB = ^AMC = 180°/2 = 90°
=. AM vuông góc với BC.
Cách 2: Vì tam giác ABC cân tại A
Mà AM là tia phân giác
=> AM đồng thời là đường cao.
=> AM vuông góc với BC .
c) Vì ∆ABC cân tại A
Mà AM vừa là đường phân giác, vừa là đường cao.
=> AM là đường trung tuyến.
=> BM = MC
Mà BM + MC = BC = 6
=> BM = MC = 6/2 = 3 ( cm )
Xét tam giác AMB vuông tại M có:
Theo định lí Pytago có:
AB² = AM² + BM²
=> AM² = AB² - BM²
Hay AM² = 5² - 3²
=> AM² = 25 - 9
=> AM² = 16
=> AM = 4 ( cm )
d) Xét tam giác ABC có:
AM vuông góc với BC
AH vuông góc với AC
Mà AM cắt AH tại H
=> H là trực tâm.
=> CH vuông góc với AB . ( Đpcm )
BA
7 tháng 5 2015
Xét 2 tam giác ABC và HBA, ta có
A= H= 900
B chung
=> tam giác ABCđồng dạng với tam giác HBA
b) Áp dụng định lí pi ta go, ta có
BC2 = AB2+AC2
BC2= 212 +282=1225
=> BC=35
... CM tương tự để ra AM và AH
27 tháng 2 2019
Vì tam giác ABC cân tại A \(\Rightarrow\widehat{B}=\widehat{C}\) mà \(\widehat{B}=50\)độ \(\Rightarrow\widehat{C}=50\)độ
ADTC tổng 3 góc trong 1 tam giác suy ra góc A = 180 - 2 lần góc B = 180- 2*50=80
b) Xét tam giác AMB và tam giác AMC có
M1=M2=90độ (vì vuông góc), AC=AB( vì tam giác ABC cân) , góc C = góc B( vì tam giác ABC cân)
suy ra tam giác AMB = tam giác AMC(ch-gn)
c) từ b suy ra MB=MC ( 2 cạnh t/ứng )
Xét tam giac IMB và tam giac IMC có
IM chung
M1=M2( vì AM vuông góc BC)
MB=MC ( chứng minh trên)
suy ra tam giác IMB = tam giác IMC (c-g-c)
suy ra góc ICM = góc IBM( 2 góc tương ứng )
suy ra tam giác IBC là tam giác cân tại I
d)( tự làm nhé)
27 tháng 2 2019
mình cần bạn nào giúp mình làm cấu d
còn những cấu trên biết làm rồi
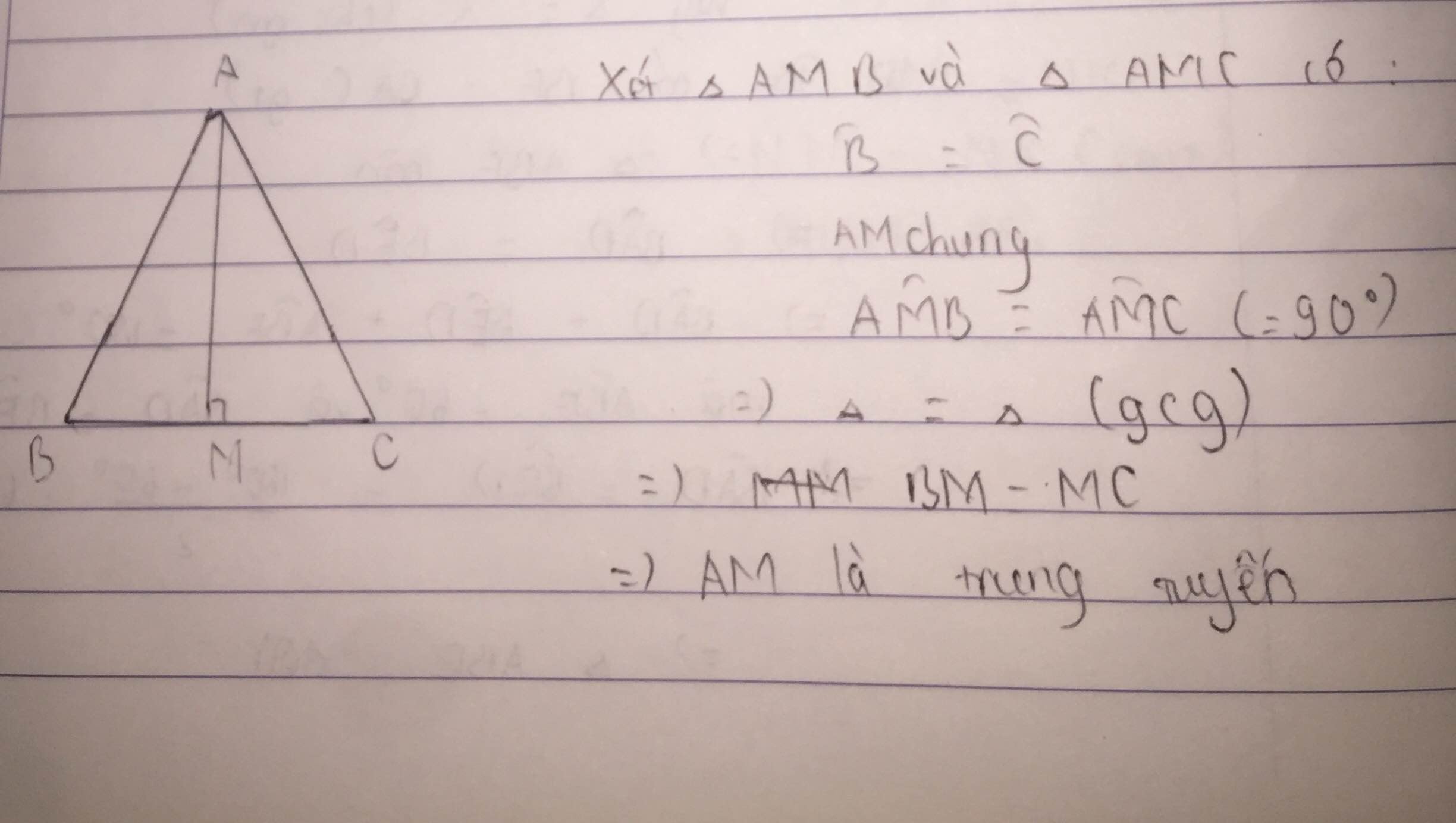
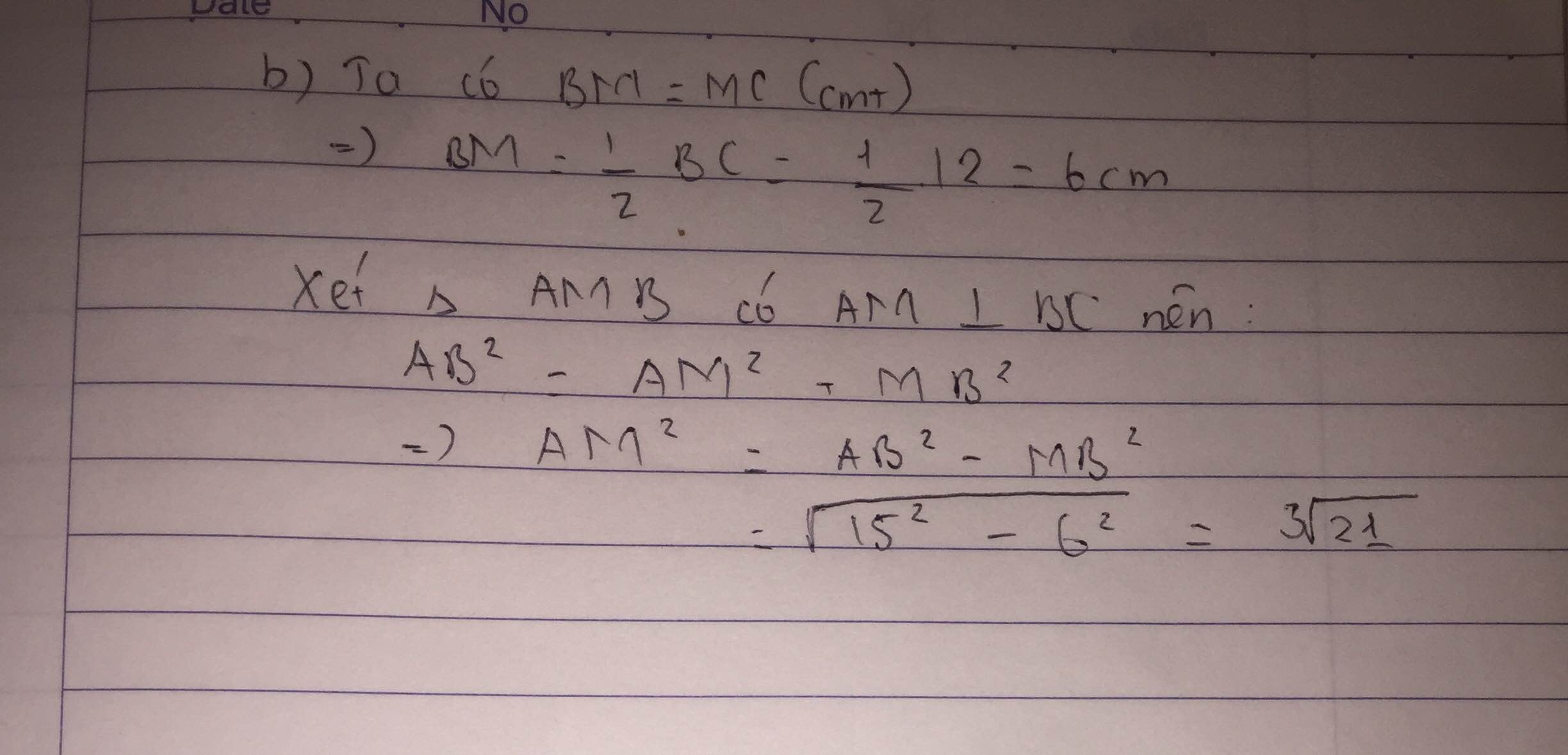
a) Xét t/giác ABM và t.giác ACM
có: AB = AC (gt)
AM : chung
BM = MC (gt)
=> t/giác ABM = t/giác ACM (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 góc t/ứng)
Mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(kề bù)
=> \(\widehat{AMB}=\widehat{AMC}=90^0\)
=> AM vuông góc với BC
b) Ta có: BM = MC = 1/2BC = 1/2.32 = 16 (cm)
Áp dụng định lí Pi - ta - go vào t/giác ABM vuông tại M, ta có:
\(AB^2=AM^2+BM^2\)
=> AM2 = AB2 - BM2 = 342 - 162 = 900
=> AM = 30 (cm)
c) Chu vi t/giác AMB = 34 + 16 + 30 = 80 (cm)
Diện tích t/giác ABM là: 30 x 16 : 2 = 240 (cm2)