Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có điểm M(-9/2;3/2) là trung điểm của cạnh AB , điểm H(-2;4) và điểm I(-1;1) lần lượt là chân đường cao kẻ từ B và tâm đường tròn ngoại tiếp tam giác ABC. Tìm tọa độ điểm C .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1

a: \(\left\{{}\begin{matrix}x_G=\dfrac{2+4+2}{3}=\dfrac{8}{3}\\y_G=\dfrac{1+0+3}{3}=\dfrac{4}{3}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x_I=\dfrac{2+4}{2}=3\\y_I=\dfrac{1+0}{2}=\dfrac{1}{2}\end{matrix}\right.\)

Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x+y+1=0\\x-2y-2=0\end{matrix}\right.\) \(\Rightarrow B\left(0;-1\right)\)
Gọi vtpt của đường thẳng CM (cũng là đường cao kẻ từ C) có tọa độ \(\left(a;b\right)\)
H là chân đường cao kẻ từ B
\(cos\widehat{HBC}=\dfrac{\left|1.1+1.\left(-2\right)\right|}{\sqrt{1^2+1^2}.\sqrt{1^2+\left(-2\right)^2}}=\dfrac{1}{\sqrt{10}}\)
\(\Rightarrow cos\widehat{MCB}=cos\widehat{HBC}=\dfrac{1}{\sqrt{10}}=\dfrac{\left|a+b\right|}{\sqrt{a^2+b^2}.\sqrt{1^2+1^2}}\)
\(\Leftrightarrow\sqrt{a^2+b^2}=\sqrt{5}\left|a+b\right|\Leftrightarrow a^2+b^2=5\left(a+b\right)^2\)
\(\Leftrightarrow2a^2+5ab+2b^2=0\Leftrightarrow\left(a+2b\right)\left(2a+b\right)=0\)
Chọn \(\left(a;b\right)=\left[{}\begin{matrix}\left(2;-1\right)\\\left(1;-2\right)\end{matrix}\right.\) (trường hợp (1;-2) loại do song song BH)
\(\Rightarrow\) Phương trình đường cao kẻ từ C:
\(2\left(x-2\right)-1\left(y-1\right)=0\Leftrightarrow2x-y-3=0\)
Tọa độ C là nghiệm: \(\left\{{}\begin{matrix}x+y+1=0\\2x-y-3=0\end{matrix}\right.\) \(\Rightarrow C\left(...\right)\)
Gọi N là trung điểm BC \(\Rightarrow\) tọa độ N
Tam giác ABC cân tại A \(\Rightarrow\) AN là trung tuyến đồng thời là đường cao
\(\Rightarrow\) Đường thẳng AN vuông góc BC \(\Rightarrow\) nhận (1;-1) là 1 vtpt và đi qua N
\(\Rightarrow\) Phương trình AN
Đường thẳng AB vuông góc CM nên nhận (1;2) là 1 vtpt
\(\Rightarrow\) Phương trình AB (đi qua B và biết vtpt)
\(\Rightarrow\) Tọa độ A là giao điểm AB và AN

a: Tọa độ trọng tâm là:
x=(1+2+0)/3=1 và y=(3+1+3)/3=7/3
c: \(d\left(A;d\right)=\dfrac{\left|1\cdot1+3\cdot\left(-1\right)+1\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{\sqrt{2}}{2}\)
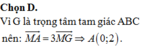


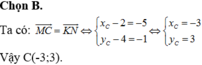

\(\overrightarrow{IM}=\left(-\frac{7}{2};\frac{1}{2}\right)=-\frac{1}{2}\left(7;-1\right)\)
M là trung điểm AB, I nằm trên trung trực AB \(\Rightarrow IM\) là trung trực AB
\(\Rightarrow\) Đường thẳng AB qua M và nhận \(\left(7;-1\right)\) là 1 vtpt
Phương trình AB:
\(7\left(x+\frac{9}{2}\right)-1\left(y-\frac{3}{2}\right)=0\Leftrightarrow7x-y+33=0\)
Do B thuộc AB nên tọa độ có dạng \(B\left(b;7b+33\right)\)
Theo công thức trung điểm: \(\left\{{}\begin{matrix}x_A=2x_M-x_B\\y_A=2y_M-y_B\end{matrix}\right.\) \(\Rightarrow A\left(-b-9;-7b-30\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}=\left(b+7;7b+34\right)\\\overrightarrow{HB}=\left(b+2;7b+29\right)\end{matrix}\right.\)
\(AH\perp BH\Rightarrow\left(b+7\right)\left(b+2\right)+\left(7b+34\right)\left(7b+29\right)=0\)
\(\Leftrightarrow50b^2+450b+1000=0\Rightarrow\left[{}\begin{matrix}b=-4\\b=-5\end{matrix}\right.\)
Tới đây xong rồi. Chia 2 trường hợp.
Biết tọa độ A;B \(\Rightarrow\) viết được pt AH \(\Rightarrow\) C thuộc AH nên đặt tọa độ C theo 1 ẩn \(\Rightarrow\) tìm tọa độ C dựa vào IA=IC
Bạn tự giải quyết nốt phần còn lại nhé