Một ca nô chuyển động đều và xuôi dòng từ A đến B mất 1h. Khoảng cách AB là 24km, vận tốc của nước so với bờ là 6km/h a) Tính vận tốc của ca nô so vs nước b) Tính thời gian để ca nô quay về từ B đến A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
14 tháng 10 2018
Sử dụng công thức cộng vận tốc: v c / b → = v c / n → + v n / b → .
a) Khi ca nô chạy xuôi dòng: v c / b = v c / n + v n / b = v c / n + 4 , 2.
Thời gian ca nô đi từ A đến B: t 1 = A B v c / b = 28 v c / n + 4 , 2 = 1 , 2.
Vận tốc của ca nô so với dòng nước: v c / n = 19 , 13 km/h.
b) Khi ca nô ngược dòng: v ' c / b = v c / n − v n / b .
Thời gian ngắn nhất để ca nô đi từ B về A:
t 2 = A B v ' c / b = A B 19 , 13 − 4 , 2 = 1 , 88 giờ ≈ 1 giờ 52 phút.
TK
1 tháng 10 2021
a,Vận tốc của ca no so với nước
ta có:\(v_t+v_n=\dfrac{s_{ab}}{t}\Rightarrow v_t+6=\dfrac{24}{1}\Rightarrow v_t=18\left(\dfrac{km}{h}\right)\)
b,Thời gian để cano quay về từ B đến A
ta có:\(v_t-v_n=\dfrac{s_{ab}}{t'}\Rightarrow18-6=\dfrac{24}{t'}\Rightarrow t'=2\left(h\right)\)
TK
8 tháng 9 2021
Chọn gốc tọa độ O trùng với A
Chiều dương trục Ox là từ A đến B
Đổi :800m=0,8 km
Phương trình chuyển động của ca nô
\(0,8=\left(21,6+2\cdot3,6\right)t=28,8t\left(km,h\right)\)
\(\Rightarrow t=\dfrac{1}{36}\left(h\right)=1'40s=100\left(s\right)\)
Vậy ...
VT
6 tháng 6 2018
Chọn B.
Khi cano chạy ngược dòng thì vận tốc cano so với bờ là
VT
15 tháng 10 2019
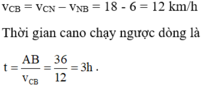
Chọn đáp án B
Vận tốc của cano so với bờ
khi chạy xuôi dòng là
Thời gian cano chạy ngược dòng là t = A B v C B = 36 12 = 3 h
VT
17 tháng 2 2017
Chọn B.
Vận tốc của cano so với bờ khi chạy xuôi dòng là vCB =AB/t=36/1,6 = 24km/h.
Vận tốc của cano so với nước là
→ vCN = vCB - vNB = 24 -6 = 18 km/h
Khi cano chạy ngược dòng thì vận tốc cano so với bờ là
vCB = vCN – vNB = 18 - 6 = 12 km/h
Thời gian cano chạy ngược dòng là
t= AB / vCB = 36/12=3h
13 tháng 6 2018
Gọi khoảng cách giữa AB là x(km).
Thời gian cano đi xuôi là: x/30(h)
Vận tốc cano ngược dòng là 20km
Vậy thời gian di ngược là x/20(h)
Thời gian xuôi ít hơn tg ngược 1h20'=4/3h nên ta có pt x/30+4/3=x/20
x = 80
a) Vận tốc của cano so với nước:
\(v_t+v_n=\dfrac{S_{AB}}{t}\Rightarrow v_t=\dfrac{S_{AB}}{t}-v_n=\dfrac{24}{1}-6=18\left(km/h\right)\)
b) Thời gian cano quay về từ B đến A:
\(v_t-v_n=\dfrac{S_{AB}}{t'}\Rightarrow t'=\dfrac{S_{AB}}{v_t-v_n}=\dfrac{24}{18-6}=2\left(h\right)\)