Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Số đo góc chưa chính xác :(
Gọi giao điểm của \(BM\) và \(CN\)là \(O\)
Từ \(O\)kẻ \(OH\)là phân giác \(\widehat{BOC}\)\(\left(H\in BC\right)\)
Xét \(\Delta ABC\)có:
\(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^o\) (định lí tổng ba góc \(\Delta\))
\(\Rightarrow\widehat{ABC}+\widehat{ACB}=180^o-60^o=120^o\)
Ta có:
\(\widehat{OBC}=\widehat{OBA}=\frac{\widehat{ABC}}{2}\) (\(OB\): phân giác \(\widehat{ABC}\))
\(\widehat{OCB}=\widehat{OCA}=\frac{\widehat{ACB}}{2}\) (\(OC\): phân giác \(\widehat{ACB}\))
\(\Rightarrow\widehat{OBC}+\widehat{OCB}=\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{120^o}{2}=60^o\)
Xét \(\Delta BOC\)có:
\(\widehat{OBC}+\widehat{OCB}+\widehat{BOC}=180^o\) (định lí tổng ba góc \(\Delta\))
\(\Rightarrow\widehat{BOC}=180^o-60^o=120^o\)
Ta có:
\(\widehat{BOH}=\widehat{HOC}=\frac{\widehat{BOC}}{2}=\frac{120^o}{2}=60^o\) (\(OH\): phân giác \(\widehat{BOC}\))
Ta có:
\(\widehat{BOC}+\widehat{BON}=180^o\) (kề bù)
\(\Rightarrow\widehat{BON}=180^o-120^o=60^o\)
\(\Rightarrow\widehat{BON}=\widehat{BOH}\left(=60^o\right)\)
Ta có:
\(\widehat{BOC}+\widehat{COM}=180^o\) (kề bù)
\(\Rightarrow\widehat{COM}=180^o-120^o=60^o\)
\(\Rightarrow\widehat{COM}=\widehat{HOC}\left(=60^o\right)\)
Xét \(\Delta BON\)và \(\Delta BOH\)có:
\(\widehat{OBN}=\widehat{OBH}\) (\(OB\): phân giác \(\widehat{ABC}\))
\(OB\): chung
\(\widehat{BON}=\widehat{BOH}\) (cmt)
\(\Rightarrow\Delta BON=\Delta BOH\left(g.c.g\right)\)
\(\Rightarrow BN=BH\) (2 cạnh tương ứng)
Xét \(\Delta COM\)và \(\Delta COH\)có:
\(\widehat{COM}=\widehat{COH}\) (cmt)
\(OC\) : chung
\(\widehat{MCO}=\widehat{HCO}\) (\(OC\): phân giác \(\widehat{ACB}\))
\(\Rightarrow\Delta COM=\Delta COH\left(g.c.g\right)\)
\(\Rightarrow MC=HC\) (2 cạnh tương ứng)
Ta có:
\(BC=BH+HC\)
Mà \(\hept{\begin{cases}BN=BH\\MC=HC\end{cases}}\)
\(\Rightarrow BC=BN+MC\left(đpcm\right)\)
a) Ta có tAx ^ + xAB ^ = 180 ∘ (hai góc kề bù) mà tAx ^ = 60 ∘
⇒ xAB ^ = 180 ∘ − 60 ∘ = 120 ∘
Mặt khác ABy ^ = 120 ∘
⇒ xAB ^ = ABy ^ mà hai góc này ở vị trí so le trong
⇒ Ax // By
b)
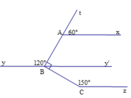
Kẻ tia By' là tia đối của tia By
Ta có: ABy ^ + ABy' ^ = 180 ∘ (hai góc kề bù) mà ABy ^ = 120 ∘
⇒ ABy' ^ = 180 ∘ − 120 ∘ = 60 ∘
Mặt khác ABC ^ = 90 ∘ hay ABy' ^ + y'BC ^ = 90 ∘
⇒ y'BC ^ = 90 ∘ − 60 ∘ = 30 ∘
Ta có y'BC ^ + CBy ^ = 180 ∘ (hai góc kề bù)
⇒ CBy ^ = 180 ∘ − 30 ∘ = 150 ∘
Ta lại có BCz ^ = 150 ∘
⇒ BCz ^ = CBy ^ mà hai góc này ở vị trí so le trong
⇒ By // Cz
a.
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{HBA}=\widehat{CDB}\) (so le trong)
Xét hai tam giác HBA và CDB có:
\(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{CDB}\left(cmt\right)\\\widehat{AHB}=\widehat{BCD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta CDB\left(g.g\right)\)
b.
Xét hai tam giác AHD và BAD có:
\(\left\{{}\begin{matrix}\widehat{ADB}\text{ chung}\\\widehat{AHD}=\widehat{BAD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AHD\sim\Delta BAD\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{DB}=\dfrac{DH}{AD}\Rightarrow AD^2=DH.DB\)
c.
Áp dụng định lý Pitago cho tam giác vuông BAD:
\(DB=\sqrt{AD^2+AB^2}=\sqrt{BC^2+AB^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Theo chứng minh câu b:
\(AD^2=DH.DB\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{BC^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông AHD:
\(AH=\sqrt{AD^2-HD^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)
a) ta có: \(\widehat{BAx}+\widehat{ABy}=60^o+120^o=180^o\)
Mà 2 góc này là 2 góc trong cùng phía ⇒Ax//By
b) ta có: \(\widehat{CBy}+\widehat{BCz}=140^o+40^o=180^o\)
Mà 2 góc này là 2 góc trong cùng phía ⇒By//Cz
c) Ax//By, By//Cz⇒Ax//Cz
cảm ơn bạn nhiều lắm ko bt bạn sinh năm bao nhiêu để dễ xưng hô