mình cần gấpppppppppppppppppppp (Vẽ hình)Bài 4. Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, Klà điểm đối xứng của điểm M qua điểm I.a) Tứ giác AMCK là hình gì? Vì sao?b) Tứ giác AKMB là hình gì? Vì sao?c) Qua C kẻ đường thẳng d song song với AB, cắt AK kéo dài tại HE, chứng minh bađường thẳng AC, BE, MK đồng...
Đọc tiếp
mình cần gấpppppppppppppppppppp (Vẽ hình)
Bài 4. Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K
là điểm đối xứng của điểm M qua điểm I.
a) Tứ giác AMCK là hình gì? Vì sao?
b) Tứ giác AKMB là hình gì? Vì sao?
c) Qua C kẻ đường thẳng d song song với AB, cắt AK kéo dài tại HE, chứng minh ba
đường thẳng AC, BE, MK đồng qui.
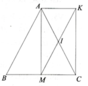
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
Xét tứ giác AMCK có
I là trung điểm của AC
I là trung điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
a, Vì I là trung điểm MK và AC nên AMCK là hbh
Mà AM là tt nên cx là đường cao
Do đó AM⊥MN nên AMCK là hcn
b, Vì AMCK là hcn nên AK//CM hay AK//MB và AK=CM=BM(do AM là tt)
Do đó AKMB là hbh