Mẫu số của một phân số (không chắc chắn là phân số tối giản) lớn hơn tử số của nó 77 đơn vị. Nếu tăng cả tử số và mẫu số thêm 22 đơn vị thì được phân số mới bằng \frac{1}{2}21.
Phân số ban đầu là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 3 2020
Gọi tử số của phâ số là a (a khác 0) -> mẫu số của phân số đó là a+9
-> phân số cần tìm có dạng : \(\frac{a}{a+9}\)
Nếu tăng cả tử và mẫu của phân số thêm 4 đơn vị thì được phân số mới bằng 1/2 nên ta có phương trình:
\(\frac{a+4}{a+9+4}\)= \(\frac{1}{2}\)
<=> \(\frac{a+4}{a+13}\)= \(\frac{1}{2}\)=> ( a+4).2=a+13 <=> 2a+8= a+ 13 <=> a= 5
=> tử số của phân số cần tìm là 5
=> mẫu số là : 5+9 =14
Vậy phân số cần tìm là 5/14
6 tháng 5 2020
Gọi tử số là x
Mẫu số là 18 + x
Theo đề ra, ta có phương trình:
\(\frac{x+2}{18+x+2}=\frac{1}{3}\)
\(\Leftrightarrow\frac{x+2}{x+20}=\frac{1}{3}\)
\(\Leftrightarrow3\left(x+2\right)=x+20\)
\(\Leftrightarrow3x+6=x+20\)
\(\Leftrightarrow3x-x=20-6\)
\(\Leftrightarrow2x=14\)
\(\Leftrightarrow x=7\)
Vậy tử số là 7, mẫu số là 18 + 7 = 25 => Phân số ban đầu là: \(\frac{7}{25}\)
CM
18 tháng 12 2017
Gọi tử số của phân số ban đầu là a, theo bài ra ta có:
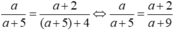
(Điều kiện: a ≠ - 5;a ≠ - 9 )
a(a + 9) = (a + 2)(a + 5)
⇔ a 2 + 9 a = a 2 + 7 a + 10
⇔ 2a = 10 ⇔ a = 5 (Thỏa mãn)
Vậy phân số cần tìm là: 5/10
21 tháng 12 2020
Gọi tử số là x.( ĐK: x thuộc Z)
=> Mẫu số là x + 3
=> Phân số ban đầu là: x/x + 3
Khi tăng cả tử và mẫu của nó thêm 2 đơn vị thì được phân số mới là:
x + 2/x + 5
=> Ta có phương trình:
x+2/x+5 = 1/2 (ĐKXĐ: x + 5 ≠ 0 <=> x ≠ -5)
<=> 2(x + 2) = x + 5
⇔ 2x + 4 = x + 5
⇔ x = 1
Vậy phân số ban đầu là : 1/4
4 tháng 2 2017
Ta có phương trình :
2x+2(x-3)=1/2
2x+2x-6=1/2
4x-6=1/2
4x=13/2
x=13/8
MD
4 tháng 2 2017
Khi tăng cả mẫu số và tử số là 2 đơn vị thì hiệu không thay đổi mà hiệu ban đầu là 3 đơn vị nên phân số mới cũng có mẫu số nhiều hơn tử số là 3 đơn vị
Vì phân số mới là 1/2 nên ta coi tử số mới là 1 phần còn mẫu số mới là 2 phần như thế
Mẫu số mới hơn tử số mới là: 2-1=1 phần
mẫu số mới là : 3*2=6
mẫu số cũ là 6-2=4
tử số cũ là 4-3=1
vậu phân số ban đầu là 1/4
