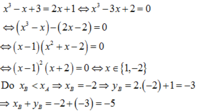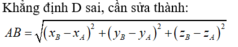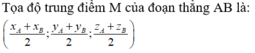Cho ba điểm A, B, C nằm trên hệ trục tọa độ Đề Các, có tọa độ lần lượt là (XA, YA), (XB, YB), (XC, YC).Tìm khoảng cách lớn nhất d giữa hai điểm trong 3 điểm trên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
Viết Chương trình diện tích tứ giác ABCD khi biết tọa độ Điểm A(xA,yA); B(xB,yB); C(xC,yC); D(xD,yD)
0
CM
19 tháng 9 2019
a) Vì A, B thuộc (P) nên:
x A = − 1 ⇒ y A = 1 2 ⋅ - 1 2 = 1 2 x B = 2 ⇒ y B = 1 2 ⋅ 2 2 = 2 ⇒ A − 1 ; 1 2 , B ( 2 ; 2 )
b) Gọi phương trình đường thẳng (d) là y = ax + b.
Ta có hệ phương trình:
− a + b = 1 2 2 a + b = 2 ⇔ 3 a = 3 2 2 a + b = 2 ⇔ a = 1 2 b = 1
Vậy (d): y = 1 2 x + 1 .
c) (d) cắt trục Oy tại điểm C(0; 1) và cắt trục Ox tại điểm D(– 2; 0)
=> OC = 1 và OD = 2
Gọi h là khoảng cách từ O tới (d).
Áp dụng hệ thức về cạnh và đường cao vào ∆ vuông OCD, ta có:
1 h 2 = 1 O C 2 + 1 O D 2 = 1 1 2 + 1 2 2 = 5 4 ⇒ h = 2 5 5
Vậy khoảng cách từ gốc O tới (d) là 2 5 5 .
CM
5 tháng 2 2017
Đáp án A
Hoành độ giao điểm của đường thẳng Δ có phương trình y = 2 x + 1 và đồ thị của hàm số y = x 3 − x + 3 là nghiệm PT:
