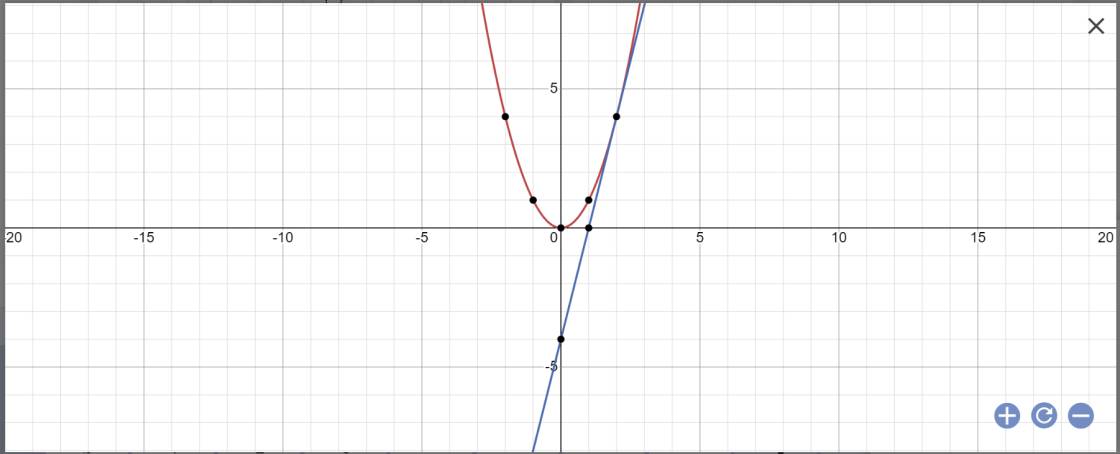
cho parabol(P) y=1/2x2 và đường thẳng (d) có phương trình y=2x-2 chứng tỏ rằng đường thẳng (d) parabol (P) có điểm chung duy nhất xác định tọa độ điểm chung đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
8 tháng 7 2021
a) Vì (d) song song với đường thẳng \(y=-2x+2003\Rightarrow\left\{{}\begin{matrix}a=-2\\b\ne2003\end{matrix}\right.\)
\(\Rightarrow\left(d\right):y=-2x+b\)
Vì (d) cắt trục hoành tại điểm có hoành độ = 1
\(\Rightarrow\) tọa độ điểm đó là \(\left(1;0\right)\)
\(\Rightarrow1=b\Rightarrow\left(d\right):y=-2x+1\)
b) pt hoành độ giao điểm: \(-\dfrac{1}{2}x^2=-2x+2\Rightarrow\dfrac{1}{2}x^2-2x+2=0\)
\(\Rightarrow x^2-4x+4=0\Rightarrow\left(x-2\right)^2=0\Rightarrow x=2\Rightarrow y=-\dfrac{1}{2}.2^2=-2\)
\(\Rightarrow\) tọa độ giao điểm là \(\left(2;-2\right)\)
TH
4 tháng 9 2020
a) Ta có: đồ thị hàm số y=ax+b đi qua điểm A (2:1)
=> 2a+b=1 (1)
Lại có: đồ thị cắt trục tung tại điểm có tung độ bằng 5
=> b=5 (2)
Từ (1) và (2) ta có: 2a+5=1
=> a= -2
b) Gía trị của m để (P) và (d) có 1 điểm chung duy nhất là
3x2 =2x+m
=> 3x2-2x-m
\(\Delta'=1+3m\)
=> m= -1/3
Tọa độ điểm chung là:
3x2=2x-1/3
=> 3x2-2x+1/3
=> x=1/3
thay x=1/3 vào vào parabol (P) ta đc: y= 3(1/3)2
y=1/3
=> Tọa độ ddiemr chung là (1/3; 1/3)
22 tháng 3 2023
a:
b: PTHĐGĐ là:
2x^2-(2m-2)x+m-1=0
Δ=(2m-2)^2-4*2*(m-1)
=4m^2-8m+4-8m+8
=4m^2-16m+12
=4m^2-2*2m*4+16-4=(2m-4)^2-4=(2m-6)(2m-2)
Để (d) cắt (P) tại 2 điểm pb thì (2m-6)(2m-2)>0
=>m>3 hoặc m<1
27 tháng 1 2023
1.2:Sửa đề: (P): y=x^2
PTHĐGĐ là:
x^2-x-m=0
Δ=(-1)^2-4*1*(-m)=4m+1
Để (P) cắt (d) tại 1 điểm duy nhất thì 4m+1=0
=>m=-1/4
MH
17 tháng 4 2022
a) Để (d) đi qua điểm A(1;3) thì \(3=2m.1+5\Rightarrow2m=-2\Rightarrow m=-1\)
b) Xét phương trình hoành độ giao điểm: \(x^2=2mx+5\)
\(\Rightarrow x^2-2mx-5=0\left(I\right)\)
Ta có \(\Delta'=m^2+5>0,\forall m\) nên PT (I) luôn có 2 nghiệm phân biệt \(x_1,x_2\) với mọi \(m\)
Vậy (d) luôn cắt (P) tại hai điểm phân biệt.
c) Áp dụng hệ thức Vi-et ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-5\end{matrix}\right.\)
Để \(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow4m^2-2.\left(-5\right)=4\Leftrightarrow4m^2=-6\) (Vô lý)
Vậy không có m thỏa mãn ycbt.
12 tháng 3 2020
a) Thay tọa dộ của điểm T vào dg thẳng d ta dc: -2.(-2) - 6 = -2 (Thỏa mãn)
Vậy điểm T có thuộc dg thẳng d
b) Pt hoành độ giao điểm của (d) và (P) là: -8x2 = -2x - 6
<=> 8x2 - 2x - 6 = 0
<=> (x - 1)(8x + 6) = 0 <=> \(\orbr{\begin{cases}x=1\\x=-\frac{3}{4}\end{cases}}\)
* Với x = 1 => y = -8
* Với x = -3/4 => y = -9/2
Tự kết luận nha
9 tháng 4 2017
Phần 1 bạn tự vẽ nhé (dùng bang giá trị)
2)Hoành độ giao điểm là ngiệm của phương trình:
2x2=4x-2
Để (d) tiếp xúc(P)<=>delta=0<=>x=1
vậy... (bạn tự viết nốt nhé!!!)
ngu the