cho tam giác abc có ab=ac. trên tia đối của tia ba lấy điểm d và trên tia đối của tia ca lấy điểm e sao cho bd=ce. CMR:a)BE=Ceb)DI=IEc)AI vông góc với BCd)BC//DE

KD

Khắc Diệu Ly

16 tháng 12 2015 - olm

cho tam giác abc có ab=ac. trên tia đối của tia ba lấy điểm d và trên tia đối của tia ca lấy điểm e sao cho bd=ce. CMR:
a)BE=Ce
b)DI=IE
c)AI vông góc với BC
d)BC//DE

#Toán lớp 7

0

PT

Pham Trong Bach

7 tháng 7 2018

Cho tam giác ABC có AB < AC. Trên tia đối của tia BC lấy điểm D sao cho BD = BA, trên tia đối của tia CB lấy điểm E sao cho CE = CA. So sánh độ dài của AD và AE

A. AD < AE

B. AD > AE

C. AD = AE

D. Không so sánh được

#Toán lớp 7

1

CM

Cao Minh Tâm

7 tháng 7 2018

Chọn A

Đúng(0)

IL

I love BTS

19 tháng 12 2018 - olm

Cho tam giác ABC có AB=AC , trên tia đối của tia BA lấy điểm D , trên tia đối của tia CA lấy điểm E sao cho BD=CE

a, Chứng minh rằng ;BE=CD

b, Chứng minh tam giác BKD = tam giác CKE ( K là giao điểm của BE và DC )

c, Chứng minh BC song song với DE

#Toán lớp 7

2

A

apple_buz

19 tháng 12 2018

a) Chứng minh rằng: BE=CD

Xét tam giác ADC và tam giác AEB, ta có

- AC = AB (đề bài cho)

- góc A chung

- AD = AB + BD, và AE = AC + CE. Mà AB = AC, BD = CE, nên AD = AE

==> tam giác ADC = tam giác AEB (cạnh - góc - cạnh)

==> BE = CD (đpcm)

2,3) mình có việc nên ko ghi ra bây giờ được

Đúng(0)

BN

Bảo Ngọc

19 tháng 12 2018

Xét ∆ ABE và ∆ ACB có :

BE = CD ( theo hình vẽ )

\(\widehat{A}\)chung

AB = AC ( gt )

=> ∆ ABE = ∆ ACB ( c.g.c )

=> BE = CD ( 2 cạnh tương ứng )

K đặt ở đâu ta :3 ?

Đúng(0)

PT

Pham Trong Bach

16 tháng 2 2019

Cho tam giác ABC cân tại A. Trên Tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của BE và CD. Chứng minh rằng BC song song DE.

#Toán lớp 7

1

CM

Cao Minh Tâm

16 tháng 2 2019

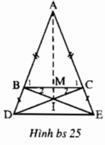
Giải sách bài tập Toán 7 | Giải bài tập Sách bài tập Toán 7

Các tam giác cân ABC và ADC có chung góc ở đỉnh ∠A nên ∠B1 = ∠ADE. Mà hai góc này ở vị trí đồng vị nên suy ra BC // DE.

Đúng(1)

P

ponpon99

13 tháng 1 2022

Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy điểm K sao cho BA = BKa/ Chứng minh tam giác BAD = BKD và b/ Trên tia đối của tia AB lấy điểm E sao cho BE = BC. Gọi I là giao điểm của tia BD với CE. Chứng minh c/ Chứng minh ba điểm K, D, E thẳng hàng.Cần gấp. Chi...

Đọc tiếp

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

13 tháng 1 2022

a: Xét ΔBAD và ΔBKD có

BA=BK

\(\widehat{ABD}=\widehat{KBD}\)

BD chung

Do đó: ΔBAD=ΔBKD

Suy ra: \(\widehat{BAD}=\widehat{BKD}=90^0\)

hay DK\(\perp\)BC

b: Xét ΔBEC có BE=BC

nên ΔBEC cân tại B

mà BI là đường phân giác

nên BI là đường cao

Đúng(0)

PQ

phạm quỳnh trang

10 tháng 4 2016 - olm

b1: cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD=CE. Vẽ DH và EK cùng vuông góc với đường thẳng BC. Chứng minh:a, HB=CKb, góc AHB = góc AKCc, HK // DED, gọi I là giao điểm DK và EH. CM: AI vuông góc với DEb2: Cho tam giác ABC vuông tại B, vẽ trung tuyến AM, trên tia đối của tia MA lấy điểm E sao cho ME=MA. CM:a, tam giác ABM= tam giác ECMb, EC vuông góc...

Đọc tiếp

#Toán lớp 7

1

TH

Thanh Hải

29 tháng 3 2021

ssssssssssssssssssssssssssssssssssssssssssssssssssssssaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii

Đúng(0)

CL

Chính Lê Hồng

24 tháng 9 2020 - olm

Cho tam giác vuông ABC (AB<AC), trên tia đối tia AB lấy điểm D sao cho BD=AC. Trên tia đối tia CA lấy điểm E sao cho CE=AB. Giao của DC và BE là F. Tính góc CFB.

#Toán lớp 8

0

CL

Chính Lê Hồng

24 tháng 9 2020 - olm

Cho tam giác vuông ABC (AB<AC), trên tia đối tia AB lấy điểm D sao cho BD=AC. Trên tia đối tia CA lấy điểm E sao cho CE=AB. Giao của DC và BE là F. Tính góc CFB.

#Toán lớp 8

0

HM

hoang minh nguyen

10 tháng 8 2021

cho tam giác ABC cân tại A trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE vẽ DH và EK cùng vuông góc với đường thẳng BC

a.HB=EK b.góc AHB = góc AKC c.HK // DE

#Toán lớp 7

2