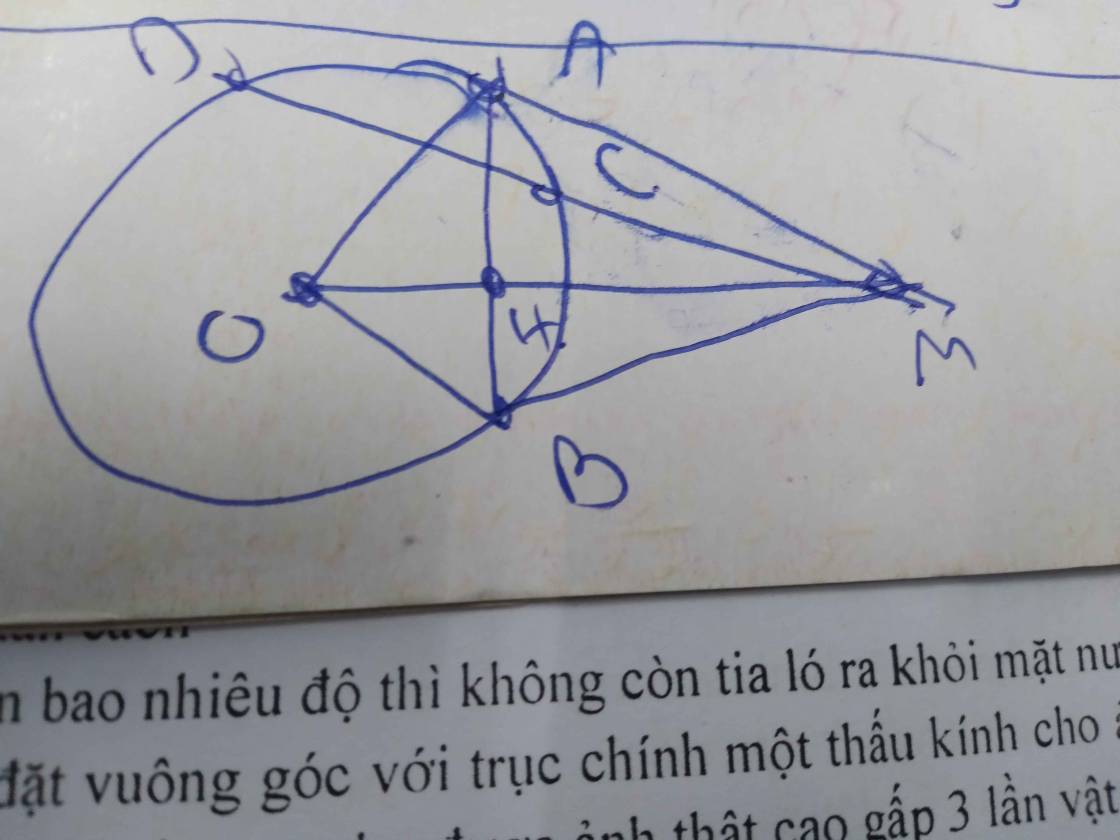
Cho đường tròn (O). Từ điểm M cố định nằm ngoài đường tròn, kẻ các cát tuyến MNP
(N nằm giữa M và P) và hai tiếp tuyến MA, MB với đường tròn (A, B là tiếp điểm, A thuộc
nửa mặt phẳng bờ MP chứa điểm O) với đường tròn (O). Gọi I là trung điểm của NP.
a) Chứng minh tứ giác MOIB nội tiếp đường tròn.
b) Chứng minh MB2 = MN. MP
c) Gọi C là giao điểm của BI với đường tròn tâm O. Chứng minh AC // MP
d) Gọi H là giao điểm của MO và AB. Khi cát tuyến MNP thay đổi thì trọng tâm tầm giác ANP chạy trên đường nào?