Cho tam giác ABC đều mà M thuộc đường ngoài ngoại tiếp tam giác
CMR: MA2+MB2+MC2=6R2 (R là bán kính đường tròn ngoại tiếp tam giác ABC)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi O là tâm đường tròn ngoại tiếp. Do tam giác ABC là tam giác đều nên O đồng thời là trọng tâm tam giác đều ABC.
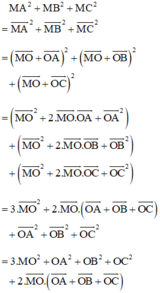
Lại có:
+ O là trọng tâm tam giác nên 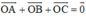
+ Bán kính đường tròn ngoại tiếp tam giác:
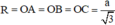
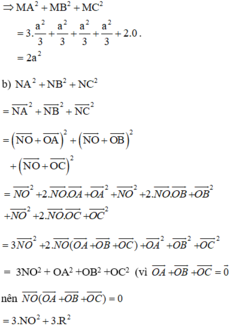
Ta có: NA2 + NB2 + NC2 ngắn nhất
⇔ NO2 ngắn nhất vì R không đổi
⇔ NO ngắn nhất
⇔ N là hình chiếu của O trên d.


Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC.
Ta có: BC = 2R
Giả sử đường tròn (O) tiếp với AB tại D, AC tại E và BC tại F
Theo kết quả câu a) bài 58, ta có ADOE là hình vuông.
Suy ra: AD = AE = EO = OD = r
Theo tính chất hai tiếp tuyến cắt nhau ta có:
AD = AE
BD = BF
CE = CF
Ta có: 2R + 2r = BF + FC + AD + AE
= (BD + AD) + (AE + CE)
= AB + AC
Vậy AB = AC = 2(R + r)

Áp dụng định lí sin trong tam giác ta có a sin A = 2 R . Suy ra:
R = a 2 sin 60 ° = a 2. 3 2 = a 3 3 .
Chọn A.

\(h=\sqrt{b^2-\frac{a^2}{4}}\Rightarrow S=\frac{1}{2}ah=\frac{1}{2}a\sqrt{b^2-\frac{a^2}{4}}\)
\(R=\frac{abb}{4S}=\frac{ab^2}{\sqrt{4b^2-a^2}.a}=\frac{b^2}{\sqrt{4b^2-a^2}}\)
\(r=\frac{S}{p}=\frac{a\sqrt{b^2-\frac{a^2}{4}}}{a+2b}\)

Gọi cạnh tam giác ABC là x
theo công thức tính diện tích S = p.r với p là nửa chu vi, r là bán kính đường tròn nội tiếp.
Ta có \(\frac{x^2\sqrt{3}}{4}=\frac{3x}{2}.1\Rightarrow x=2\sqrt{3}\) (cm)
Suy ra bán kính đường tròn ngoại tiếp : \(R=\frac{AB.BC.AC}{4.S_{ABC}}\frac{x^3}{\frac{4.x^2\sqrt{3}}{4}}=\frac{x}{\sqrt{3}}=2\) (cm)

Theo định lí sin trong tam giác ta có:
a sin A = 2 R ⇒ R = a 2 sin A = 6 2. sin 60 0 = 2 3
Chọn B.
Bài toán phụ: Cho tam giác ABC có \(\widehat{A}=120^o\). Khi đó BC2=AB2+AC2+AB.AC
Chứng minh: Gọi H là hình chiếu của C trên AB
\(AH=\frac{1}{2}AC;CH=\frac{\sqrt{3}}{2}AC\left(1\right)\)
Theo định lý Pytago, ta có: BC2=BH2+CH2 (2)
Từ (1)(2) => BC2=(AB+AH)2+CH2=\(\left(AB+\frac{1}{2}AC\right)^2+\left(\frac{\sqrt{3}}{2}AC\right)^2\)
\(=AB^2+AB\cdot AC+\frac{1}{4}AC^2+\frac{3}{4}AC^2=AB^2+AC^2+AB\cdot AC\)
Không mất tính tổng quát giả sử M thuộc cung \(\widebat{BC}\) (không chứa A) của (O)
Chứng minh được MA=MB+MC
=> MA2=MB2+MC2+2.MB.MC
=> MA2+MB2+MC2=2(MB2+MC2+MB.MC)(3)
Theo BĐ1 ta có: MB2+MC2+MB.MC=BC2
=> MB2+MC2+MB.MC=3R2
Từ (1) (2) => MA2+MB2+MC2=6R2