Cho tam giác ABC có AB=9 cm,AC=6cm,BC=10 cm.Tia phân giác của góc BAC cắt cạnh BC ở D.Tia phân gicas góc ngoài của óc BAC cắt BC tại E.Tính dộ dài đoạn BE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 8 2015
AE là phân giác BAC
=> \(\frac{EB}{EC}=\frac{AB}{AC}=\frac{5}{6}\)
=> \(\frac{EB}{5}=\frac{EC}{6}=\frac{EB+EC}{5+6}==\frac{BC}{11}=\frac{7}{11}\) ( Áp dụng dãy tỉ số bàng nhau )
=> EB = 7/11 . 5 = 35/11
=> EC = 7/11 . 6 = 42 / 11
29 tháng 2 2016
phuong trinh:
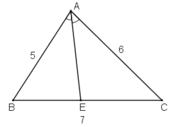
BE/BA=CE/CA(THEO TINH CHAT DUONG PHAN GIAC CUA TAM GIAC)
Hay BE/5=CE/7
Ap dung tinh chat cua day ti so bang nhau ta co:
BE/5=CE/7=(BE+CE)/5+7=BC/12=7/12
Tu BE/5=7/12=>BE=(7*5)/12=35/12
CE/7=7/12=>CE=(7*7)/12=49/12
10 tháng 5 2016
Ta có: AE là phân giác góc BAC nên theo tính chất phân giác, ta có:
\(\frac{EB}{EC}=\frac{AB}{AC}=\frac{5}{6}\)
\(=>\frac{EB}{5}=\frac{EC}{6}=\frac{EB+EC}{5+6}=\frac{BC}{11}=\frac{7}{11}\)
\(=>EB=\frac{35}{11}\)
\(=>EC=\frac{42}{11}\)
10 tháng 3 2023
11:
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot6\cdot12}{6+12}\cdot\dfrac{1}{2}=4\left(cm\right)\)
12:
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot3\cdot6}{3+6}\cdot\dfrac{1}{2}=\dfrac{3\cdot6}{3+6}=\dfrac{18}{9}=2\left(cm\right)\)
22 tháng 4 2017
AE là đường phân giác của tam giác ABC nên
=
Áp dụng tính chất tỉ lệ thức
= = =
=> EB = =
EC = BC- BE ≈ 3,8
Lời giải:
Theo tính chất đường phân giác trong:
BDDC=ABAC=69=23BDDC=ABAC=69=23
⇒BDBD+DC=22+3=25⇒BDBD+DC=22+3=25
⇔BDBC=25⇒BD=BC.25=3⇔BDBC=25⇒BD=BC.25=3 (cm)
Theo tính chât phân giác ngoài:
EBEC=ABAC=69=23EBEC=ABAC=69=23
⇔EBEB+BC=23⇔EBEB+BC=23
⇔EBEB+7,5=23⇔EBEB+7,5=23
⇒3EB=2(EB+7,5)⇒EB=15⇒3EB=2(EB+7,5)⇒EB=15 (cm)
Ta có: ED=EB+BD=15+3=18ED=EB+BD=15+3=18 (cm)