Bài 01. Vẽ đường tròn (O) rồi lấy bốn điểm A, B, C, D phân biệt trên đường tròn đó. Vẽ các dây cung có hai đầu là hai trong bốn điểm đã cho. Hỏi trong hình vẽ có:
a) Bao nhiêu dây cung?
b) Bao nhiêu cung tròn?
c) Bao nhiêu tam giác có các đỉnh là ba trong bốn điểm trên?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 5 2022
a: Tên các cung là CA;AD;CB;DB
b: Vì AB là đường kính
và CD là dây
nên AB>CD
c: Ta sẽ được n(n-1) cung
CM
13 tháng 5 2017
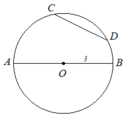
Với hai điểm (phân biệt) trên một đường tròn ta có được 2 cung có mút là hai điểm đó. Với n điểm (phân biệt) cho trước trên một đường tròn, thì cứ lấy 2 trong số n điểm đó ta được 2 cung, vì vậy có tất cả n(n-1) cung trên đường tròn đó.
CM
6 tháng 5 2017
Giả sử vẽ được như hình bs.18
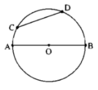
Với hai điểm (phân biệt) trên một đường tròn ta có được hai cung có mút là hai điểm đó. Với n điểm (phân biệt) cho trước trên một đường tròn, thì cứ lấy 2 trong số n điểm đó ta được 2 cung, vì vậy có tất cả n(n – 1) cung trên đường tròn đó.
CM
20 tháng 5 2019
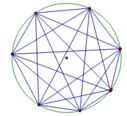
a/ Lấy 7 điểm phân biệt thuộc một đường tròn như hình vẽ
b/ Trên hình có 42 cung
c/ Vẽ các dây cung tạo thành từ các cặp điểm trên như hình vẽ
d/ Trên hình có tất cả 21 dây cung.
mk cố nghĩ nhưng mk chịu rồi,mk kém hình lắm.
Đoán xem