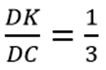Cho tam giác ABC vuông tại A. Gọi D là trung điểm BC. Qua D kẻ DM AB (M AB), DN
AC (N AC) .
a) Chứng minh tứ giác ANDM là hình chữ nhật.
b) Gọi I là điểm đối xứng của D qua N. Tứ giác DAIC là hình gì ? Tại sao?
c) Tìm điều kiện của tam giác ABC để tứ giác ANDM là hình vuông.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
16 tháng 12 2015
a) Ta có: MD vuông góc với ab
dn vuông góc với ac
nên: góc dma và góc dna =90 độ
và góc bac = 90 vì tam giác abc vuông tại a
vậy tứ giác là hcn (tg có 3 góc vuông)
b) đầu tiên bạn chứng minh DN là đường trung bình của tam giác abc suy ra DN // BA
Sau đó bạn c/m hbh có 2 đg chéo cắt nhau tại trung điểm của mỗi đường
mà BA vuông góc AC => DN vuông góc AC
Mà n là trung điểm DI (......)
SUY RA: DN vuông góc với AC
Vậy hbh ADCI là hình thoi (hbh có 2 đg chéo vuông góc với nhau)
26 tháng 7 2022
a: Xét tứ giác AMDN có góc AMD=góc AND=góc MAN=90 độ
nên AMDN là hình chữ nhật
b: Xét tứ giác NKIM có
D là trung điểm của NI
D là trung điểm của KM
Do đó: NKIM là hình bình hành
mà NI vuông góc với KM
nên NKIM là hình thoi
c: Xét ΔABC có DN//AB
nên DN/AB=CN/CA=CD/CB
=>CN=1/2CA
hay N là trung điểm của AC
Xét ΔABC có DM//AC
nên BM/BA=BD/BC=1/2
hay BM=1/2BA
=>M là trung điểm của AB
Ta có: ΔAHB vuông tại H
mà HM là đường trung tuyến
nên MA=MH
Ta có: ΔAHC vuông tại H
mà HN là đừog trung tuyến
nên HN=AN
Xét ΔMAN và ΔMHN có
MA=MH
AN=HN
MN chung
Do đó: ΔMAN=ΔMHN
Suy ra:góc MHN=90 độ
16 tháng 1 2022
a: Xét tứ giác AMIN có
\(\widehat{AMI}=\widehat{ANI}=\widehat{NAM}=90^0\)
Do đó:AMIN là hình chữ nhật
b: Xét tứ giác ADCI có
N là trung điểm của AC
N là trung điểm của DI
Do đó: ADCI là hình bình hành
mà IA=IC
nên ADCI là hình thoi
c: AB=15cm
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=15\cdot10=150\left(cm^2\right)\)
LN
14 tháng 2 2022
TK
a) Xét tứ giác AMIN có:
∠(MAN) = ∠(ANI) = ∠(IMA) = 90o
⇒ Tứ giác AMIN là hình chữ nhật (có 3 góc vuông).
b) ΔABC vuông có AI là trung tuyến nên AI = IC = BC/2
do đó ΔAIC cân có đường cao IN đồng thời là đường trung tuyến
⇒ NA = NC.
Mặt khác ND = NI (t/c đối xứng) nên ADCI là hình bình hành
Lại có AC ⊥ ID (gt). Do đó ADCI là hình thoi.
c) Ta có: AB2 = BC2 – AC2 (định lí Py-ta-go)
= 252 – 202 ⇒ AB = √225 = 15 (cm)
Vậy SABC = (1/2).AB.AC = (1/2).15.20 = 150 (cm2)
d) Kẻ IH // BK ta có IH là đường trung bình của ΔBKC
⇒ H là trung điểm của CK hay KH = HC (1)
Xét ΔDIH có N là trung điểm của DI, NK // IH (BK // IH)
Do đó K là trung điểm của DH hay DK = KH (2)
Từ (1) và (2) ⇒ DK = KH = HC ⇒ DK/DC= 1/3.
CH
Cô Hoàng Huyền
Admin
VIP
26 tháng 2 2018
Em tham khảo tại đây nhé.
Câu hỏi của nguuen thi minh tam - Toán lớp 8 - Học toán với OnlineMath
2 tháng 1 2023
a: D đối xứng M qua AB
nên AD=AM; BD=BM và DM vuông góc với AB
Xét tứ giác AIDE có
góc AID=góc AED=góc EAI=90 độ
Do đó: AIDE là hình chữ nhật
b: AD=AM
BD=BM
mà AD=BD
nên AD=AM=BD=BM
=>ADBM là hình thoi
c: AI=AB/2=3cm
AE=AC/2=4,5cm
SAIDE=3*4,5=13,5cm2
12 tháng 1 2022
a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó: E là trung điểm của AB
Xét tứ giác AIBD có
E là trung điểm của AB
E là trung điểm của ID
Do đó: AIBD là hình bình hành
mà AB\(\perp\)DI
nên AIBD là hình thoi
