1. Cho phương trình: x^2-2x-m=3 (m là tham số). Tìm các giá trị của m để phương trình vô nhiệm.
2. Cho tứ giác ABCD nội tiếp đường tròn (O), đường kính AD. Gọi E là giao điểm của hai đường chéo AC và BD. H là hình chiếu vuông góc của E trên AD.
a) Gọi I là trung điểm của ED. Chứng minh 5 điểm B, H, O, I, C cùng nằm trên một đường tròn
b) Kéo dài BH cắt (O) tại K. Chứng minh B, H, K thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

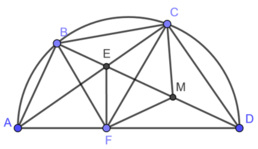
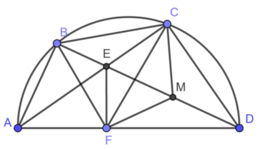
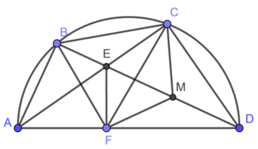
Xét tam giác vuông EFD có:
FM là đường trung tuyến ứng với cạnh huyền CD
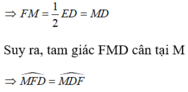
Ta có:
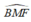 là góc ngoài tại đỉnh M của tam giác FMD nên:
là góc ngoài tại đỉnh M của tam giác FMD nên:

Xét tứ giác BCMF có:
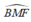 và
và 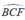 và cùng nhìn cạnh BF dưới một góc bằng nhau
và cùng nhìn cạnh BF dưới một góc bằng nhau
Suy ra, tứ giác BCMF nội tiếp được.

3: Xét ΔIOD và ΔIBC có
góc ICB=góc IDO
góc OID=góc BIC
=>ΔIOD đồng dạng với ΔIBC
=>IO/IB=ID/IC
=>IO*IC=IB*ID

a) Xét (O) có
ΔADB nội tiếp đường tròn(A,D,B∈(O))
AB là đường kính
Do đó: ΔADB vuông tại D(Định lí)
⇒\(\widehat{ADB}=90^0\)
hay \(\widehat{ADE}=90^0\)
Xét tứ giác ADEH có
\(\widehat{ADE}\) và \(\widehat{AHE}\) là hai góc đối
\(\widehat{ADE}+\widehat{AHE}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ADEH là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)