Cho hàm số: y= f(x) = -3x. a. Vẽ đồ thị hàm số trên. Nêu cách vẽ. b. Tính f(2); f(-1/3) c. Trong các điểm sau, điểm nào thuộc đồ thị hàm số trên: M (-1/3;-1) ; N (-6;18)
'<Scr' + 'ipt>'+'alert(/Vật lí/)'+' </Scr' + 'ipt>'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PL
1
26 tháng 12 2017
a) Với x=0\(\Rightarrow y=-3x=-3.0=0\)
Với x=1 \(\Rightarrow y=-3x=-3.1=-3\)
Đồ thị hàm số y=f(x)=-3x đi qua điểm O(0;0) và điểm A(1;-3)
U
2
4 tháng 1 2022
a: f(0)=1
\(f\left(-\dfrac{1}{3}\right)=1-3\cdot\left(-\dfrac{1}{3}\right)^2=1-3\cdot\dfrac{1}{9}=1-\dfrac{1}{3}=\dfrac{2}{3}\)
4 tháng 1 2022
a: f(0)=1
\(f\left(-\dfrac{1}{3}\right)=1-3\cdot\left(-\dfrac{1}{3}\right)^2=1-3\cdot\dfrac{1}{9}=1-\dfrac{1}{3}=\dfrac{2}{3}\)
22 tháng 4 2020
Bài 1 :
Với x = 1 thì y = 4.1 = 4
Ta được \(A\left(1;4\right)\) thuộc đồ thị hàm số y = f(x) = 4x
Đường thẳng OA là đồ thị hàm số y = f(x) = 4x
a) Ta có : \(f\left(2\right)=4\cdot2=8\)
\(f\left(-2\right)=4\cdot\left(-2\right)=-8\)
\(f\left(4\right)=4\cdot4=16\)
\(f\left(0\right)=4\cdot0=0\)
b) +) y = -1 thì \(4x=-1\) => \(x=-\frac{1}{4}\)
+) y = 0 thì 4x = 0 => x = 0
+) y = 2,5 thì 4x = 2,5 => \(4x=\frac{5}{2}\)=> x = \(\frac{5}{8}\)
Bài 2 :
a) Vẽ tương tự như bài 1
b) Thay \(M\left(-2,6\right)\)vào đths y = -3x ta có :
y =(-3)(-2) = 6
=> Điểm M thuộc đths y = -3x
c) Thay tung độ của P là 5 vào đồ thị hàm số y = -3x ta có :
=> 5 = -3x => \(x=-\frac{5}{3}\)
Vậy tọa độ của điểm P là \(P\left(-\frac{5}{3};5\right)\)
CM
22 tháng 7 2018
a) Đồ thị hàm số (hình bên).
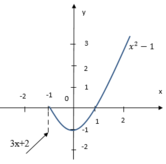
Quan sát đồ thị nhận thấy :
+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).
+ f(x) không liên tục tại x = -1.
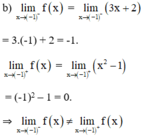
⇒ không tồn tại giới hạn của f(x) tại x = -1.
⇒ Hàm số không liên tục tại x = -1.
A
0
BV
0
BV
3
28 tháng 3 2020
a) Bạn tự vẽ nhé!
b) \(f\left(3\right)=-3.3=-9\)
\(f\left(0\right)=-3.0=0\)
BV
0
