Tìm m để hàm số y=\(\sqrt{x^2-2mx-2m+3}\) có tập xác định là R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = \(\sqrt{x^2-2mx-2m+3}\) có tập xác định là R
1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2022
Hàm có TXĐ là R khi và chỉ khi \(x^2-2mx-2m+3\ge0;\forall x\)
\(\Leftrightarrow\Delta'=m^2+2m-3\le0\)
\(\Leftrightarrow-3\le m\le1\)
14 tháng 3 2021
Hàm số có tập xác định là R \(\Leftrightarrow x^2-2mx-2m+3\ge0\forall x\in R\)
\(\Leftrightarrow\Delta'=m^2+\left(2m-3\right)\leq0\)
\(\Leftrightarrow\left(m-1\right)\left(m+3\right)\le0\Leftrightarrow-3\le m\le1\).
Các gt nguyên âm của m thoả mãn là : -3; -2; -1.
Vậy có 3 gt nguyên âm của m thoả mãn.
9 tháng 10 2021
Hàm số xác định khi \(\left\{{}\begin{matrix}x^2+2mx+2018m+2019>0\\mx^2+2mx+2020\ge0\end{matrix}\right.\)
Xét \(f\left(x\right)=x^2+2mx+2018m+2019\)
Có: \(\Delta'=m^2-2018m-2019\)
Để \(f\left(x\right)>0\) thì \(\Delta'< 0\Leftrightarrow m^2-2018m-2019< 0\Leftrightarrow-1< m< 2019\)(*)
Xét \(g\left(x\right)=mx^2+2mx+2020\)
Dễ thấy \(m=0\) thì \(g\left(x\right)=\sqrt{2020}>0\)(1)
Để \(g\left(x\right)\ge0\) thì \(\left\{{}\begin{matrix}m>0\\\Delta'\le0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m^2-2020m\le0\end{matrix}\right.\)\(\Leftrightarrow0< m\le2020\) (2)
(1),(2)\(\Rightarrow g\left(x\right)\ge0\Leftrightarrow0\le m\le2020\) (**)
(*),(**) suy ra hàm số xác định khi \(0\le m< 2019\)
Do đó tập hợp các giá trị nguyên của m để hàm số xác định là:
\(S=\left\{m\in Z|0\le m< 2019\right\}\) và tập hợp có 2019 phần tử
H
1
2 tháng 7 2023
ĐKXĐ: 2m-3sinx>=0
=>3sin x<=2m
=>sin x<=2m/3
mà -1<=sin x<=1
nên -1<=2m/3<=1
=>-3<=2m<=3
=>-3/2<=m<=3/2
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 12 2022
Hàm xác định trên R khi và chỉ khi:
\(8cosx-6sinx-\left(3sinx-4cosx\right)^2-2m\ge0;\forall x\) (1)
Đặt \(3sinx-4cosx=t\)
\(\Rightarrow t^2=\left(3sinx-4cosx\right)^2\le\left(3^2+\left(-4\right)^2\right)\left(sin^2x+cos^2x\right)=25\)
\(\Rightarrow-5\le t\le5\)
(1) tương đương:
\(-2t-t^2-2m\ge0;\forall t\in\left[-5;5\right]\)
\(\Leftrightarrow2m\le-t^2-2t;\forall t\in\left[-5;5\right]\)
\(\Leftrightarrow2m\le\min\limits_{t\in\left[-5;5\right]}\left(-t^2-2t\right)\)
Xét hàm \(f\left(t\right)=-t^2-2t\) trên \(\left[-5;5\right]\)
\(-\dfrac{b}{2a}=-1\) ; \(f\left(-5\right)=-15\) ; \(f\left(-1\right)=1\) ; \(f\left(5\right)=-35\)
\(\Rightarrow2m\le-35\Rightarrow m\le-\dfrac{35}{2}\)
V
2
30 tháng 6 2021
Đặt \(t=cosx;t\in\left[-1;1\right]\)
Để hàm số có tập xác định R
\(\Leftrightarrow cosx^2-\left(2+m\right)cosx+2m\ge0;\forall x\)
\(\Leftrightarrow t^2-\left(2+m\right)t+2m\ge0\) với mọi \(t\in\left[-1;1\right]\)
Đặt \(f\left(t\right)=t^2-\left(2+m\right)t+2m\); \(I\left(\dfrac{2+m}{2};f\left(\dfrac{2+m}{2}\right)\right)\)
TH1: \(\dfrac{2+m}{2}< -1\) \(\Leftrightarrow m< -4\)
Để \(f\left(t\right)\ge0;\forall t\in\left[-1;1\right]\) \(\Leftrightarrow\)\(f\left(t\right)_{min}=f\left(-1\right)\ge0\) \(\Leftrightarrow3+3m\ge0\Leftrightarrow m\ge-1\)(ktm đk)
TH2: \(-1\le\dfrac{m+2}{2}\le1\)\(\Leftrightarrow-4\le m\le0\)
Để \(f\left(t\right)\ge0;\forall t\in\left[-1;1\right]\) \(\Leftrightarrow f\left(t\right)_{min}=f\left(\dfrac{2+m}{2}\right)\ge0\)\(\Leftrightarrow-m^2+4m-4\ge0\)\(\Leftrightarrow m=2\) (ktm đk)
TH3:\(\dfrac{m+2}{2}>1\) \(\Leftrightarrow m>0\)
Để \(f\left(t\right)\ge0;\forall t\in\left[-1;1\right]\)\(\Leftrightarrow f\left(t\right)_{min}=f\left(1\right)\ge0\)\(\Leftrightarrow m-1\ge0\Leftrightarrow m\ge1\)
Kết hợp cả ba TH \(\Rightarrow m\ge1\)
Vậy...
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 6 2021
Đơn giản hơn:
\(t^2-\left(m+2\right)t+2m\ge0\) ; \(\forall t\in\left[-1;1\right]\)
\(\Leftrightarrow t\left(t-2\right)-m\left(t-2\right)\ge0\)
\(\Leftrightarrow\left(t-m\right)\left(t-2\right)\ge0\) (1)
Do \(t-2< 0\) ; \(\forall t\in\left[-1;1\right]\) nên (1) tương đương:
\(t-m\le0\)
\(\Leftrightarrow m\ge t\) ; \(\forall t\in\left[-1;1\right]\)
\(\Rightarrow m\ge1\)
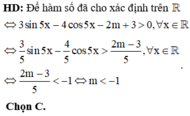
jup mình vs các bạn
Để hàm số \(y=\sqrt{x^2-mx-2m+3}\) có tập xác định là R thì:
\(x^2-mx-2m+3\ge0\)
Ta có:\(\Delta_x=m^2-4\left(3-2m\right)\ge0\)
\(\Leftrightarrow m^2-8m-12\ge0\)
\(\Leftrightarrow\left(m^2-2\cdot4m+16\right)-28\ge0\)
\(\Leftrightarrow\left(m-4\right)^2\ge28\)
\(\Leftrightarrow-\sqrt{28}+4\le m\le\sqrt{28}+4\)
P/S:Số xấu,không chắc