( 6x3 - 7x2 - x + 2 ) : ( 2x + 1 )
giúp mk với
hì hì ^^
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
3
21 tháng 5 2022
137,4 + x + 179,3 + x + 13 = 196
2x + 329,7 = 196 2x = 196 - 329,7 2x = - 133,7 x = - 133,7 : 2 x = - 66,85
BH
21 tháng 5 2022
137,4 + x + 179,3 + x + 13=196
(x+x) + (137,4+179,3+13)=196
x x 2 + 329,7=196
x x 2=196-329,7=-133,7
x=-133,7:2
x=-66,85
Học tốt :)))))
9 tháng 12 2021
\(=\left(6x^3+3x^2-10x^2-5x+4x+2\right):\left(2x+1\right)\\ =\left[3x^2\left(2x+1\right)-5x\left(2x+1\right)+2\left(2x+1\right)\right]:\left(2x+1\right)\\ =3x^2-5x+2\)
10 tháng 11 2021
\(=12x^3-10x+18x^2-15\)
\(\left(6x^3-7x^2-x+2\right):\left(2x+1\right)\\ =\left[\left(6x^3-6x^2\right)-\left(x^2-x\right)-\left(2x-2\right)\right]:\left(2x+1\right)\\ =\left[\left(x-1\right)\left(6x^2-x-2\right)\right]:\left(2x+1\right)\\ =\left\{\left(x-1\right)\left[\left(6x^2+3x\right)-\left(4x+2\right)\right]\right\}:\left(2x+1\right)\\ =\left[\left(x-1\right)\left(3x-2\right)\left(2x+1\right)\right]:\left(2x+1\right)\\ =\left(x-1\right)\left(3x-2\right)\)
30 tháng 11 2021
\(=\dfrac{6x^3+3x^2-10x^2-5x+4x+2}{2x+1}=3x^2-5x+2\)
CM
18 tháng 12 2018
Cách 1: Thực hiện phép chia
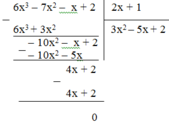
Vậy (6x3 – 7x2 – x + 2) : (2x + 1) = 3x2 – 5x + 2
Cách 2: Phân tích 6x3 – 7x2 – x + 2 thành (2x + 1).P(x) + R(x)
6x3 – 7x2 – x + 2
= 6x3 + 3x2 – 10x2 – 5x + 4x + 2
(Tách -7x2 = 3x2 – 10x2; -x = -5x + 4x)
= 3x2.(2x + 1) – 5x.(2x + 1) + 2.(2x + 1)
= (3x2 – 5x + 2)(2x + 1)
Vậy (6x3 – 7x2 – x + 2) : (2x + 1) = 3x2 – 5x + 2
Giải thích cách tách:
Vì có 6x3 nên ta cần thêm 3x2 để có thể phân tích thành 3x2(2x + 1). Do đó ta tách -7x2 = 3x2 – 10x2.
Lại có -10x2 nên ta cần thêm -5x để có thể phân tích thành -5x(2x + 1). Do đó ta tách –x = -5x + 4x.
Có 4x, ta cần thêm 2 để có 2.(2x + 1) nên 2 không cần phải tách.
\(\frac{6x^3-7x^2-x+2}{2x+1}\)
= \(\frac{\left(6x^3+3x^2\right)-\left(10x^2+5x\right)+\left(4x+2\right)}{2x+1}\)
= \(\frac{3x^2\left(2x+1\right)-5x\left(2x+1\right)+2\left(2x+1\right)}{2x+1}\)
= \(\frac{\left(2x+1\right)\left(3x^2-5x+2\right)}{2x+1}\)
= 3x2 - 5x + 2
= ( 3x2 - 3x ) - ( 2x - 2 )
= 3x ( x - 1 ) - 2 ( x - 1 )
= ( x - 1 ) ( 3x - 2 ).