rút gọn biểu thức
2-(y+44)+31
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. `A=2x^2y(-3xy)=-6x^3y^2`
Bậc: `3+2=5`
2. Thay `x=-1, y=3` vào A: `A=-6.(-1)^3.3^2=54`

Lời giải:
1. \(P=\left[\frac{1}{\sqrt{x}(\sqrt{x}-1)}+\frac{\sqrt{x}}{\sqrt{x}(\sqrt{x}-1)}\right]:\frac{x}{(\sqrt{x}-1)^2}\)
\(=\frac{\sqrt{x}+1}{\sqrt{x}(\sqrt{x}-1)}.\frac{(\sqrt{x}-1)^2}{x}=\frac{(\sqrt{x}+1)(\sqrt{x}-1)}{x\sqrt{x}}=\frac{x-1}{x\sqrt{x}}\)
2.
\(P>\frac{1}{2}\Leftrightarrow \frac{x-1}{x\sqrt{x}}> \frac{1}{2}\)
\(\Leftrightarrow \frac{2x-2-x\sqrt{x}}{2x\sqrt{x}}>0\)
\(\Leftrightarrow 2x-2-x\sqrt{x}>0\)
\(\Leftrightarrow x\sqrt{x}+2< 2x\)
Điều này vô lý do theo BĐT Cô-si thì:\(x\sqrt{x}+2=\frac{x\sqrt{x}}{2}+\frac{x\sqrt{x}}{2}+2\geq 3\sqrt[3]{\frac{x^3}{2}}>\frac{3x}{\sqrt[3]{2}}> 2x\)
Vậy không tồn tại $x$ thỏa mãn.
1) Ta có: \(P=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{x}{x-2\sqrt{x}+1}\)
\(=\left(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\right)\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{x}\)
\(=\dfrac{x-1}{x\sqrt{x}}\)


2/5 x 1/2 : 1/3 = 2/5 x 1/2 x 3 = 3/5
1/2 x 1/3 + 1/4= 1/6 + 1/4 = 4/24 + 6/24 = 10/24 =5/12

\(3\left(x-y\right)^2-2\left(x+y\right)^2-\left(x+y\right)\left(x-y\right)\)
\(=3.\left(x^2-2xy+y^2\right)-2\left(x^2+2xy+y^2\right)-x^2+y^2\)
\(=3x^2-6xy+3y^2-2x^2-4xy-2y^2-x^2+y^2\)
\(=2y^2-10xy\)

Ta có A=1/5+1/20+1/44+...+1/170
=>A=1/10+1/40+1/88+...+1/340
A=\(\frac{1}{2.5}\)+\(\frac{1}{5.8}\)+\(\frac{1}{8.11}\)+......+\(\frac{1}{17.20}\)
A=1/3.(1/2-1/5+1/5-1/8+1/8-1/11+.....+1/17-1/20)
A=1/3.(1/2-1/20)
A=\(\frac{3}{20}\)

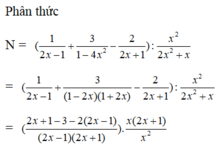
= 2 x + 1 − 3 − 4 x + 2 2 x − 1 2 x + 1 . 2 x + 1 x = − 2 x 2 x − 1 2 x + 1 . 2 x + 1 x = − 2 2 x − 1
Vậy N = 2 1 − 2 x
Đáp án cần chọn là B
2-(y+44)+31
=2-y-44+31
=-y-11
\(=2-\left(y+44\right)+31\)
\(=2-y-44+31\)
\(=-y-11\)