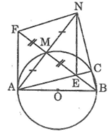
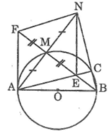
Cho đường tròn (O,R) đường kính AB. Một điểm M nằm trên đường tròn( M khác A,B ). Gọi N là điểm đối xứng của A qua điểm M. Gọi E là giao điểm của đường thẳng BM với tiếp tuyến A của đường tròn (O).
1. Nếu góc ABE bằng 60 độ và R = 3cm. Tính độ dài đoạn thẳng EA và Eb
2. Chứng minh EN vuông góc với NB
3. Chứng minh En là tiếp tuyến của đường tròn (B;2R)