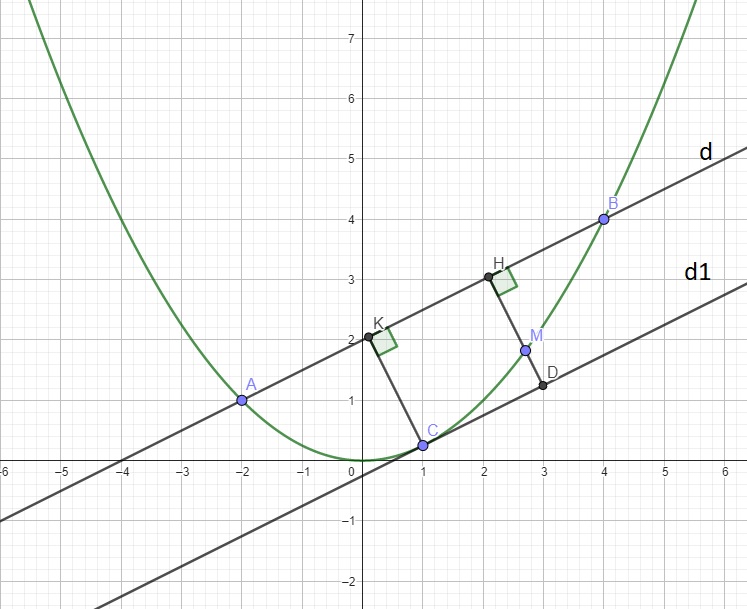
Cho parabol (P): y = 1/4x^2 và đường thẳng (D) qua 2 điểm A và B trên (P) có hoành độ lần lượt là -2 và 4 a) Khảo sát sự biến thiên b) Viết phương trình của (D) c) Tìm điểm M trên cung AB của (P) (tương ứng hoành độ) x € [-2;4] sao cho tam giác MAB có diện tích lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
a. Em tự giải
b. Từ giả thiết ta có \(A\left(-2;1\right)\) và \(B\left(4;4\right)\)
Gọi phương trình (d) có dạng \(y=ax+b\), do (d) qua A và B nên:
\(\left\{{}\begin{matrix}-2a+b=1\\4a+b=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=2\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x+2\)
c. Câu này có vài cách giải cho lớp 9, cách nhanh nhất là sử dụng tính chất tiếp tuyến.
Từ M kẻ \(MH\perp AB\Rightarrow S_{ABM}=\dfrac{1}{2}MH.AB\)
Do AB cố định \(\Rightarrow S_{max}\) khi \(MH_{max}\)
Gọi \(d_1\) là đường thẳng song song d và tiếp xúc (P), gọi C là tiếp điểm \(d_1\) và (P)
Do \(d_1\) song song (d) nên pt có dạng: \(y=\dfrac{1}{2}x+b\)
Phương trình hoành độ giao điểm \(d_1\) và (P):
\(\dfrac{1}{4}x^2=\dfrac{1}{2}x+b\Rightarrow x^2-2x-4b=0\) (1)
Do \(d_1\) tiếp xúc (P) \(\Rightarrow\left(1\right)\) có nghiệm kép
\(\Rightarrow\Delta'=1+4b=0\Rightarrow b=-\dfrac{1}{4}\)
Thế vào (1) \(\Rightarrow x_C^2-2x_C+1=0\Rightarrow x_C=1\Rightarrow y_C=\dfrac{1}{4}\) \(\Rightarrow C\left(1;\dfrac{1}{4}\right)\)
Từ C kẻ \(CK\perp d\)
Giả sử HM kéo dài cắt \(d_1\) tại D \(\Rightarrow\) tứ giác CKHD là hình chữ nhật (2 cặp cạnh đối song song và 1 góc vuông)
\(\Rightarrow CK=DH\)
Mà \(DH=MH+MD\ge MH\Rightarrow CK\ge MH\)
\(\Rightarrow MH_{max}=CK\) khi M trùng C
Hay \(M\left(1;\dfrac{1}{4}\right)\)
19 tháng 5 2021
b) Thay x=-4 vào (P), ta được:
\(y=\dfrac{-1}{4}\cdot\left(-4\right)^2=\dfrac{-1}{4}\cdot16=-4\)
Thay x=2 vào (P), ta được:
\(y=\dfrac{-1}{4}\cdot2^2=\dfrac{-1}{4}\cdot4=-1\)
Vậy: A(-4;-4) và B(2;-1)
Gọi (d): y=ax+b(a\(\ne\)0) là phương trình đường thẳng đi qua hai điểm A và B
\(\Leftrightarrow\left\{{}\begin{matrix}-4a+b=-4\\2a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6a=-3\\2a+b=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=-1-2a=-1-2\cdot\dfrac{1}{2}=-1-1=-2\end{matrix}\right.\)
Vậy: (d): \(y=\dfrac{1}{2}x-2\)
31 tháng 5 2017
câu a :
Vì \(a=\frac{1}{4}>0\)nên đồ thị hàm số có đồ thị nằm phía trên trục hoành và có đỉnh parabol đi qua gốc tọa độ (0,0)
bảng giá trị :
| x | -4 | -2 | 0 | 2 | 4 |
| y | 4 | 1 | 0 | 1 | 4 |
Đồ thị
Qua đồ thị ta thấy khi \(x\in\left(-\infty;0\right)\)hàm nghịch biến ; \(x\in\left(0;\infty\right)\)hàm số đồng biến
Câu b:
gọi phương trình đường thẳng d dạng: \(y=ax+b\)
Xét tại A (-2;y1) :\(y_1=\frac{\left(-2\right)^2}{4}=1\)
Xét tạ B(4;y2) : \(y_2=\frac{4^2}{4}=4\)
do đó tọa độ đường thẳng A,B thỏa mãn đường thẳng d nên có hệ :
\(\hept{\begin{cases}-2a+b=1\\4a+b=4\end{cases}\Leftrightarrow\hept{\begin{cases}a=\frac{1}{2}\\b=2\end{cases}}}\)
vậy phương trình d : \(y=\frac{1}{2}x+2\)
L
4 tháng 2 2020
Bài 3:
Đặt \(a=m^2-4\)
\(a)\) Đồ thị hàm số \(y=\left(m^2-4\right)x-5\)nghịch biến
\(\Leftrightarrow a< 0\)
\(\Leftrightarrow m^2-4< 0\)
\(\Leftrightarrow m^2< 4\)
\(\Leftrightarrow-\sqrt{4}< m< \sqrt{4}\)
\(\Leftrightarrow-2< m< 2\)
Vậy với \(-2< m< 2\)thì hàm số nghịch biến
\(b)\) Đồ thị hàm số \(y=\left(m^2-4\right)x-5\)đồng biến \(\forall x>0\)
\(\Leftrightarrow a>0\)
\(\Leftrightarrow m^2-4>0\)
\(\Leftrightarrow m^2>4\)
\(\Leftrightarrow\orbr{\begin{cases}m>2\\m< -2\end{cases}}\)
Vậy với \(\orbr{\begin{cases}m>2\\m< -2\end{cases}}\)thì hàm số đồng biến \(\forall x>0\)
22 tháng 5 2015
a) (P) là parabol đi qua gốc toạ độ O(0; 0) ; điểm (1; 1/2) và điểm (-1;1/2)
b) A \(\in\) (P) => yA = \(\frac{1}{2}\). xA2 = \(\frac{1}{2}\). (-1)2 = \(\frac{1}{2}\)=> A (-1; \(\frac{1}{2}\))
B \(\in\) (P) => yB = \(\frac{1}{2}\).xB2 = \(\frac{1}{2}\).4 = 2 => B (2; 2)
+) đường thẳng có hệ số góc bằng \(\frac{1}{2}\) có dạng y = \(\frac{1}{2}\)x + b (d)
A \(\in\) d => yA = \(\frac{1}{2}\).xA + b => \(\frac{1}{2}\) = \(\frac{1}{2}\). (-1) + b => b = 1
Vậy đường thẳng (d) có dạng y = \(\frac{1}{2}\)x + 1
Nhận xét: yB = \(\frac{1}{2}\).xB + 1 => B \(\in\) (d)
