Cho tam giác ABC, K là trung điểm của AB, E là trung điểm của AC. Trên tia đối của tia KC lấy điểm M sao cho KM = KB. Trên tia đối của tia EB lấy điểm N sao cho EN = EB. Chứng minh rằng:
a) Tam giác KAM = tam giác KBC và tam giác EAN = tam giác ECB
b) AM = AN
c) AM // BC ; AN // BC
d) A là trung điểm của MN

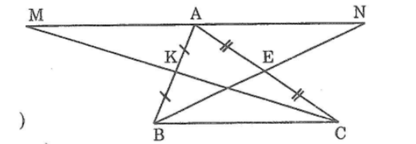

Giải:
Xét ΔAMK,ΔBCKΔAMK,ΔBCK có:
AK=KB(=12AB)AK=KB(=12AB)
K1ˆ=K2ˆK1^=K2^ ( đối đỉnh )
MK=KC(gt)MK=KC(gt)
⇒ΔAMK=ΔBCK(c−g−c)⇒ΔAMK=ΔBCK(c−g−c)
⇒A1ˆ=Bˆ⇒A1^=B^ ( góc t/ứng )
Xét ΔANE,ΔCBEΔANE,ΔCBE có:
AE=EC(=12AC)AE=EC(=12AC)
E1ˆ=E2ˆE1^=E2^ ( đối đỉnh )
BE=EN(gt)BE=EN(gt)
⇒ΔANE=ΔCBE(c−g−c)⇒ΔANE=ΔCBE(c−g−c)
⇒A2ˆ=Cˆ⇒A2^=C^ ( góc t/ứng )
Ta có: Aˆ+Bˆ+Cˆ=180oA^+B^+C^=180o ( tổng 3 góc của ΔABCΔABC )
⇒Aˆ+A1ˆ+A2ˆ=180o⇒A^+A1^+A2^=180o
⇒MANˆ=180o⇒MAN^=180o
⇒M,A,N⇒M,A,N thẳng hàng (1)
Vì ΔAMK=ΔBCKΔAMK=ΔBCK
⇒MA=BC⇒MA=BC ( cạnh t/ứng )
Vì ΔANE=ΔCBEΔANE=ΔCBE
⇒AN=BC⇒AN=BC
⇒MA=AN(=BC)⇒MA=AN(=BC) (2)
Từ (1) và (2) ⇒A⇒A là trung điểm của MN
Vậy A là trung điểm của MN