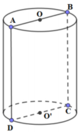
Từ một khoanh giò hình trụ, người ta cắt rời ra phần thẳng đứng theo các bán kính OA, OB. Cho biết diện tích xung quanh của khoanh giò sau khi cắt rời một phần ra đúng bằng diện tích xung quanh trước khi cắt. Tính góc AOB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 3 2020
Xem tại đây nhé: https://hoc24.vn/hoi-dap/question/935790.html
CM
19 tháng 12 2017
Phần diện tích xung quanh còn lại (không kể phần lõm)
S 1 = 2. π .3.4. (11/12) =22π ( c m 2 )
Diện tích còn lại của hai đáy :
S 2 = 2. π . 3 2 . (11/12) =33 π 2 ( c m 2 )
Diện tích phần lõm là diện tích của hai chữ nhật kích thước 3cm và 4cm
S 3 = 2.3.4=24 ( c m 2 )
Diện tích toàn bộ hình sau khi đã cắt:
CM
21 tháng 5 2019
Hình nón được tạo thành có độ dài đường sinh là l = OA = 2, chu vi đường tròn đáy bằng độ dài cung AB và bằng
CM
22 tháng 2 2018
Đáp án B
Theo bài ra, ta có R = a S = 8 a 2 ⇒ S = h .2 R = 8 a 2 ⇒ h = 4 a .
Vậy diện tích xung quanh của hình trụ là S x q = 2 π R h = 8 π a 2
CM
4 tháng 11 2018
S A B C D = 8 a 2 ⇒ 2 a . h = 8 a 2 ⇔ h = 4 a
Diện tích xung quanh của hình trụ:
S x q = 2 πRh = 2 π . a . 4 a = 8 πa 2
Thể tích khối trụ
V t r ụ = πR 2 h = πa 4 . 4 a = 4 πa 3
Chọn đáp án C.
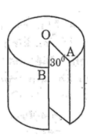
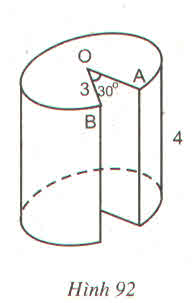
Ta đặt \(\widehat{AOB}=n^o\) thì sđ \(\stackrel\frown{AB}=n^o\)
Diện tích xung quanh bị mất đi một phần là:
\(S_1=\dfrac{\pi.R.n}{180}.h\)
Diện tích xung quanh được thêm một phần mới là:
\(S_2=2R.h\)
Theo đề bài thì \(S_1=S_2\)
\(\Leftrightarrow \dfrac{\pi Rn.h}{180}=2R.h\\ \Leftrightarrow \pi Rnh=360Rh\\ \Leftrightarrow n=\dfrac{360}{\pi} \approx 144^o39'\)