Question

[•๖ۣۜHυүềη ²ƙ⁷ ( ๖ۣۜTεαм ๖ۣۜBạ¢ɦ ๖ۣۜ...]

Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm. Gọi I là giao điểm của ba đường phân giác, M là trung điểm của cạnh BC. Tia BI cắt AC tại D. Chứng minh rằng:

a)       Tam giác ABC vuông tại A.

b)      Góc AIC và góc BDC bằng nhau.

c)       5AD = 3DC.

d)      Tam giác BIM vuông tại I

ai giỏi vào giúp mk đi ạ

Answer 1

[Kiệt Nguyễn]

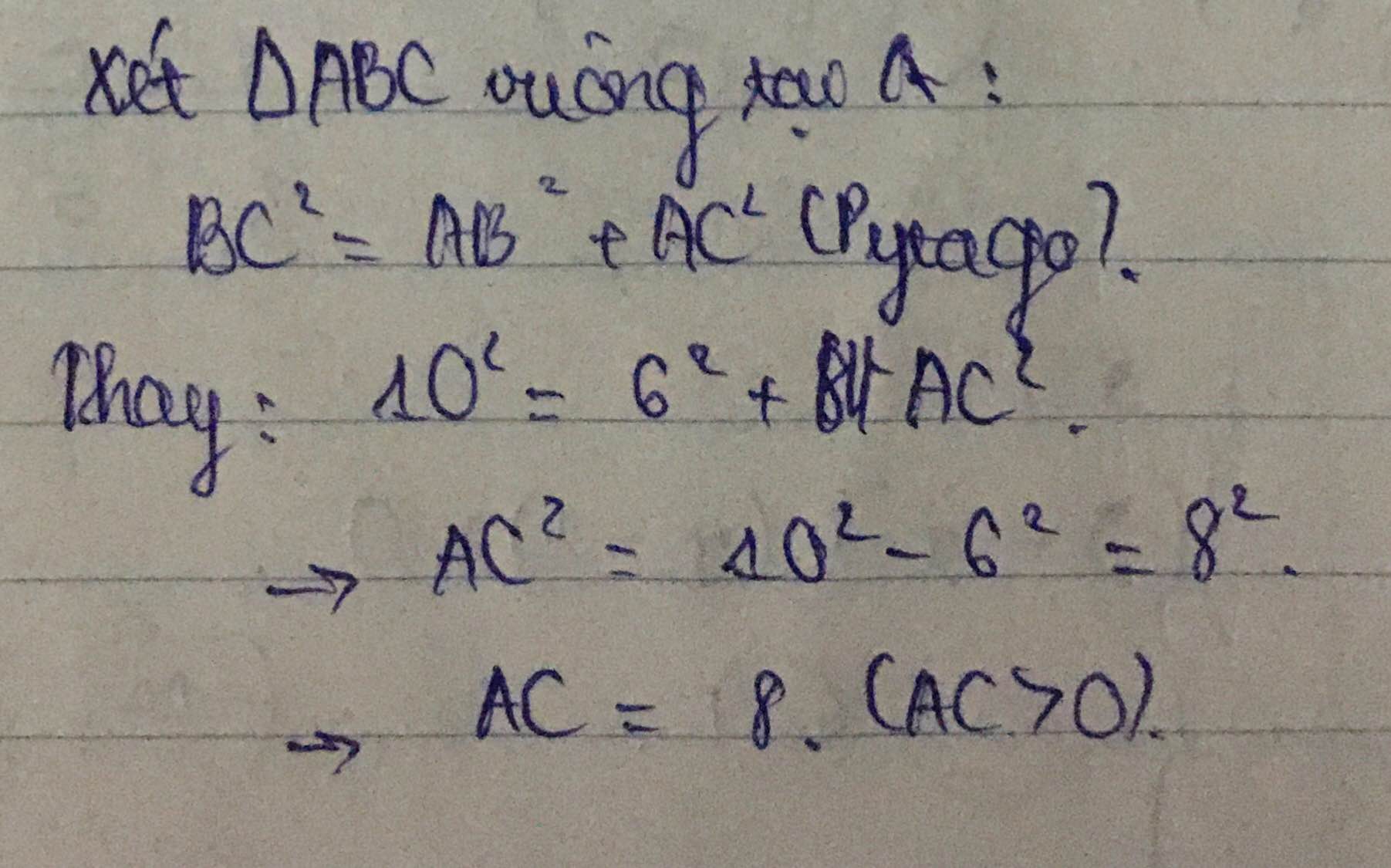
P/S: Một bài toán rất hay của toán lớp 7 khi phải dùng t/c đường phân giác dùng ở lớp 8, mình đã chứng minh t/c đó bằng cách lớp 7 nên bạn cứ yên tâm sử dụng khi thi!

a) \(\Delta\)ABC có AB² + AC² = 6² + 8² = 100

và BC² = 10² = 100

=> AB² + AC² = BC²

=> \(\Delta\)ABC vuông tại A (định lý Pythagoras đảo)

b) CI và AI là hai đường phân giác của \(\Delta\)ABC nên ^AIC = 90⁰ + \(\frac{\widehat{B}}{2}\)

Mà ^BDC = 90⁰ + \(\frac{\widehat{B}}{2}\)(tính chất góc ngoài) nên ^AIC = ^BDC (đpcm)

c) Trên BC lấy K sao cho BA = BK

Dễ chứng minh \(\Delta\)ABD = \(\Delta\)ABK (c.g.c)

=> \(S_{\Delta ABD}=S_{\Delta ABK}\)và AD = KD (hai cạnh tương ứng)

Ta có: \(\frac{S_{\Delta ABD}}{S_{\Delta BDC}}=\frac{AD}{DC}\)(vì có cùng chiều cao hạ từ B)

\(\frac{S_{\Delta BDK}}{S_{\Delta BDC}}=\frac{BK}{BC}\)(vì có cùng chiều cao hạ từ D)

Từ đó suy ra \(\frac{AD}{DC}=\frac{BK}{BC}\Rightarrow\frac{AD}{DC}=\frac{BA}{BC}=\frac{6}{10}\)

\(\Rightarrow10AD=6DC\Rightarrow5AD=3DC\left(đpcm\right)\)

d) Từ câu c) dễ tính được DC = 5cm

=> \(\Delta\)MIC = \(\Delta\)DIC (c.g.c) => ^IMC = ^IDC (hai góc tương ứng)

=> ^BDA = ^IMB

=> ^IBM + ^IMB = ^ABD + ^BDA = 90⁰

Vậy \(\Delta\)BIM vuông tại I (đpcm)