cho đường tròn tâm O đường kính AB. Qua trung điểm E của OB, kẻ một dường thẳng vuông góc OB, cắt đường tròn O ở M và N. Kẻ dây MP song song AB. Gọi I là điểm chính giữa của cung nhỏ PM. K là giao điểm của OI và PM. CM: KE song song PN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
Hà Đức Thọ
Admin
VIP
20 tháng 1 2021
Thọ tested! h heeeee
\(\sqrt{2222}\)
\(\dfrac{1}{22}\)
6 tháng 2 2021
Giải :
a) Xét (O) có PM // AB
⇒ 2 cung AP và BM bị chắn bởi 2 dây trên sẽ bằng nhau.
mà BM = BN ( △ BMN cân tại B vì có BE vừa là đ/c, đường trung tuyến △)
⇒ cung BM = cung BN
⇒ cung AP = cung BN
b) Xét (O) có OI đi qua điểm chính giữa của PM (gt)
⇒ OI vuông góc với dây PM tại K
⇒góc OKM = 90 độ.
Xét tứ giác OKME có 3 góc vuông : góc OKM = 90 độ (cmt),
góc MEO = 90 độ ( MN vuông góc với OB tại E
góc EMK = 90 độ ( vì PM//AB, AB vuông góc với MN ⇒ PM vuông góc với MN tại M )
⇒ OKME là hcn
c) Ta có : góc OPI = góc NOE ( vì 2 góc đông vị, MP//AB)
mà góc OPI + góc POI = 90 độ ( △POK vuông tại K )
⇒góc NOE + góc POI = 90 độ
⇒ góc NOE + góc POI + góc IOE = 90 + 90 = 180 độ
⇒ P,O,N thẳng hàng
- Xét △ PMN có KE đường TB ( K trđ PM, E trđ MN )
⇒ KE//PN
3 tháng 7 2023
a: C là điểm chính giữa của cung AB
=>OC vuông góc AB
góc OHE=góc OME=90 độ
=>OHME nội tiếp
b: góc AMB=1/2*sđ cung AB=90 độ
=>góc AMH+góc AOH=180 độ
=>OHMA nội tiếp
=>O,H,M,E,A cùng thuộc 1 đường tròn
=>góc EAO=90 độ
OHEA có 3 góc vuông
=>OHEA là hcn
=>EH=OA=R
CM
18 tháng 1 2018
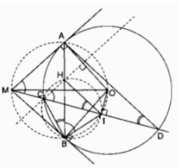
A, B, I nhìn MO cố định dưới một góc bằng 90° nên A, B, I nằm trên đường tròn bán kính MO.
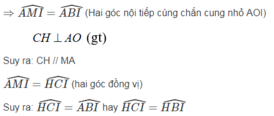
B và C cùng nằm trên một nửa mặt phẳng bờ chứa đường HI tạo với HI một góc bằng nhau nên tứ giác BCHI nội tiếp.
