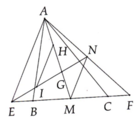
Cho tam giác ABC, M là trung điểm của BC. D là điểm bất kì trên tia đối của tia BA. Gọi H và K lần lượt là hình chiếu của B và C trên đường thẳng DM. Gọi G là trọng tâm của tam giác ABC. Chứng minh G là trọng tâm của tam giác AHK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

NM
Nguyễn Minh Quang
Giáo viên
4 tháng 4 2021
Gọi G là trọng tâm của tam giác ABC\(\frac{\Rightarrow AG}{AM}=\frac{2}{3}\)
Ta có \(\hept{\begin{cases}BM=CM\\\widehat{BHM}=\widehat{CKM}=90^0\\\widehat{BMH}=\widehat{CMK}\end{cases}\Rightarrow\Delta BHM=\Delta CKM\left(\text{ cạnh huyền - góc nhọn}\right)}\)
Vì vậy \(HM=KM\) nên AM là trung tuyến của \(\Delta AHK\) mà \(\frac{AG}{AM}=\frac{2}{3}\Rightarrow G\) là trọng tâm tam giác AHK