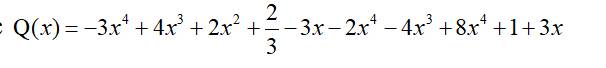a, thu gọn và sắp xếp các đa thức trên lũy thừa giảm dần bậc của biến. .b, tính tổng P(x) + Q(x) rồi tìm nghiệm của đa thức tổng
Vài giây trước
![]()
_Ác★Quỷ★Tỏa★Nắng✔™♈_♥ (# nhạt #)
cj nghĩ là cj dell lm dc
1 phút trước
![]()
Nguyễn Lê Tuấn Anh
P(x) =3x mũ 3 - 2x + 2+ x mũ 2 - 3x mũ 3 + 2x mũ 2 + 3 + x. Q(x) 5x mũ 3 - x mũ 2 + 3x - 5x mũ 3 + 4 -x mũ 2 + 2x - 2