Question

[Lê Hoàng Quân]

Câu 1 : Cho tam thức bậc hai f(x)=-x²+(m+2)x-4. Tìm các giá trị của tham số m để :

a) Phương trình f(x)=0 có hai nghiệm phân biệt

b) Tam thức f(x)<0 với mọi x

Câu 2 : Cho bất phương trình 2x²+(m-1)x+1-m >0

a) Giải bất phương trình (1) với m=2

b) Tìm m để bất phương trình (1) nghiệm đúng với mọi giá trị của x

Câu 3 : Cho f(x)=(m-1)x²-2(m-1)x-1. Tìm m để bất phương trình f(x)>0 vô nghiệm.

Answer 1

[Phan Trân Mẫn]

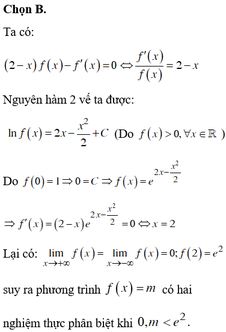
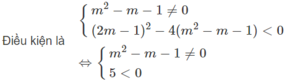
Câu 1 : a/Δ Δ = (m+2)² - 4(-1)(-4) = m² +2m -12
ycbt <=> Δ > 0 <=> m² +2m-12 > 0
<=> m < -1-\(\sqrt{13}\) ; m > -1+\(\sqrt{13}\)
Vậy giá trị cần tìm m ∈ (-∞; -1-\(\sqrt{13}\) ) U (-1+\(\sqrt{13}\) ; +∞)

b/ Δ = m² +2m-12
ycbt <=> Δ < 0 <=> m² +2m-12 < 0
<=> -1-\(\sqrt{13}\)<m< -1+\(\sqrt{13}\)

Answer 2

[Phan Trân Mẫn]

Câu 2 .
a/ Thay m=2 vào bpt ta được : 2x²+(2-1)x+1-2 >0
<=> 2x² + x -1 > 0 <=> x < -1 ; x > \(\frac{1}{2}\)