Cho hình vuông ABCD cạnh a. E là điểm nằm giữa A và B, đường thẳng CE cắt đường thẳng AD tại K. Qua C kẻ đường thẳng vuông góc với CE, cắt AB tại I.
a) CMR: Trung điểm của IK di động trên 1 đường thẳng cố định khi E di động trên đoạn AB.
b) Cho BE=x. TÍnh BK, IK, CK và diện tích tứ giác ACKI theo a và x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: H và D đối xứng với nhau qua AB
nên AH=AD; BH=BD
=>ΔHAD cân tại A
=>AB là phân giác của góc HAD(1)
Ta có H và E đối xứngvới nhau qua AC
nên AH=AE; CH=CE
=>ΔAHE cân tại A
=>AC là phân giác của góc HAE(2)
Từ (1) và (2) suy ra góc DAE=2xgóc BAC=180 độ
=>D,A,E thẳng hàng
b: Xét ΔAHB và ΔADB có
AH=AD
BH=BD
AB chung
Do đó: ΔAHB=ΔADB
Suy ra: góc ADB=90 độ
=>BD vuông góc với DE(3)
Xét ΔAHC và ΔAEC có
AH=AE
HC=EC
AC chung
Do đó: ΔAHC=ΔAEC
Suy ra: góc AEC=90 độ
=>CE vuông góc với ED(4)
Từ (3) và (4) suy ra BDEC là hình thang vuông
c: ED=AE+AD
=AH+AH=2AH
d: Xét ΔDHE có
HA là đường trung tuyến
HA=DE/2
Do đó: ΔDHE vuông tại H

Câu hỏi của Nguyễn Thành Nam - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại link trên nhé.

Trong tam giác DKL vuông tại D với đường cao DC. Theo định lí 4, ta có:
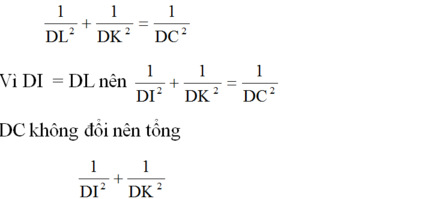
không đổi khi I thay đổi trên cạnh AB. (đpcm)