Một kỳ nghỉ ở trên biển , và bên cạnh bãi biển là một cái khách sạn 4 sao . Ở trong khách sạn có 345 người , ở bãi biển , số người gấp đôi số người ở trong khách sạn . Biết rằng số nam bằng 3/4 số nữ . Hỏi có bao nhiêu nam ,bao nhiêu nữ ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có sơ đồ:
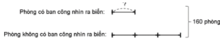
Số phần bằng nhau là:
1 + 3 = 4 (phần)
Số phòng có ban công nhìn ra biển là :
160 : 4 = 40 (phòng)
Đáp số : 40 phòng.

A -> TRUNG QUỐC -> THỨ 16
D -> AI CẬP -> THỨ 10
C -> ĐỨC -> THỨ 8
B -> MEXICO -> THỨ 4
A -> TRUNG QUỐC -> THỨ 16
D -> AI CẬP -> THỨ 10
C -> ĐỨC -> THỨ 8
B -> MEXICO -> THỨ 4

Đáp án B.
Ta gọi A D = x 0 ≤ x ≤ 50 (km)
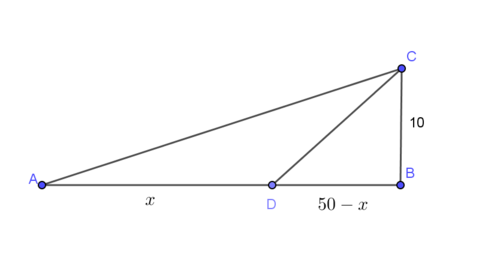
Khi đó: B D = 50 − x ; C D = 100 + 50 − x 2
Từ đó chi phí đi lại là:
f x = 3. x + 5. 100 + 50 − x 2 = 3 x + 5 x 2 − 100 x + 2600
Ta cần tìm để chi phí này là thấp nhất.
Ta có: f ' x = 3 + 5 2 x − 100 2 x 2 − 100 x + 2600 ;
f ' x = 0 ⇔ 6 x 2 − 100 x + 2600 = 500 − 10 x
⇔ x = 42 , 5.
Ta có: f 0 , f 2 < f 42 , 5
Vậy A D = 42 , 5 = 85 2 thì chi phí đi lại là thấp nhất.

Đáp án B
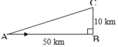
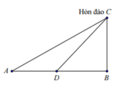
Đặt A D = x ⇒ B D = A B − A D = 40 − x ⇒ C D = B D 2 + B C 2 = 40 − x + 10 2
Suy ra kinh phí người đó phải bỏ là T = 3 x + 5 x 2 − 80 x + 1700 → f x
Khảo sát hàm số f(x)trên (0;40) suy ra min f x = 160 ⇔ x = 65 2 k m
Và chi phí người đó chỉ đi đường thủy là t = 5 40 2 + 10 2 = 500 17 U S D
VẬY kinh phí nhỏ nhất cần bỏ ra khi đi đường bộ là 65/2

Đặt giá phòng là x. Thu nhập f(x)
bài toán được phát biểu lại dưới dạng thuần túy Toán học như sau:
Tìm x sao cho f(x) lớn nhất biết rằng khi x = 400 thì f(400) = 400x50, mỗi khi x tăng thêm 20 đơn vị thì f(x+20k) = (x+20k)x(50-2k).
Giá đã tăng: x - 400 (ngàn đồng).
Số phòng cho thuê giảm nếu giá là x:

Số phòng cho thuê với giá x là:

Trả lời câu 1: Thay giá trị x = 500 vào biểu thức trên ta được giá trị cần tìm là 40.
Doanh thu là: f(x) =

Trả lời câu 2: Thế f(x) = 20200 vào phương trình trên, giải phương trình bậc hai, ta được x = 427,64 hoặc x= 472,36
f’(x)=

f’’(x)= -1/5
f’(x) = 0, tương đương x = 450.
và f’’(450) = -1/5< 0
Trả lời câu 3: Theo trên thì x = 450 là cực đại và là cực trị duy nhất.
Tuấn Anh Phan Nguyễn
Đặt giá phòng là x. Thu nhập f(x)
Bài toán được phát biểu lại dưới dạng thuần túy toán học như sau:
Tìm x sao cho f(x) lớn nhất biết rằng khi x = 400 thì f(400) = 400x50, mỗi khi x tăng thêm 20 đơn vị thì f(x+20k) = (x+20k)x(50-2k).
Giá đã tăng: x - 400 (ngàn đồng).
Số phòng cho thuê giảm nếu giá là x:

Số phòng cho thuê với giá x là:

Trả lời câu 1: Thay giá trị x = 500 vào biểu thức trên ta được giá trị cần tìm là 40.
Doanh thu là: f(x) =

Trả lời câu 2: Thế f(x) = 20200 vào phương trình trên, giải phương trình bậc hai, ta được x = 427,64 hoặc x= 472,36
f’(x)=

f’’(x)= -1/5
f’(x) = 0, tương đương x = 450.
và f’’(450) = -1/5< 0
Trả lời câu 3: Theo trên thì x = 450 là cực đại và là cực trị duy nhất.
tự lm nha bé :))