Question

[Tiến Nguyễn Minh]

Bài 3. Cho hình chữ nhật ABCD. Gọi M, N lần lượt là trung điểm AD, BC. E là một điểm nằm trên tia đối của tia DC. Dựng tia Nx sao cho NM là phân giác ∠xNE. Nx giao EM tại K. Chứng minh rằng A, K, C thẳng hàng.

 Bài 4. Cho tam giác ABC, trực tâm H. M là trung điểm BC. Qua H kẻ một đường thẳng cắt hai cạnh AB, AC tại E, F sao cho HE = HF. Chứng minh rằng MH ⊥ EF.

Bài 5. Cho tam giác ABC. M, N, P lần lượt là các điểm trên cạnh BC, CA, AB. AM giao BN tại I, BN giao CP tại J, CP giao AM tại K. Biết SAIN = SBJP = SCKM = SIJK. Chứng minh rằng SAIJP = SBJKM = SCKIN .

Bài 6. Cho tam giác ABC có trực tâm H. M là điểm nằm trong tam giác sao cho ∠ABM = ∠ACM. Kẻ ME ⊥ AC, MF ⊥ AB. Gọi K là trực tâm tam giác AEF. Chứng minh rằng K, M, H thẳng hàng.

Answer 1

[Thanh Tùng DZ]

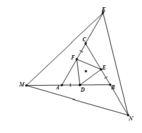
bài 3

Gọi giao điểm của EM với AC là K' ( K' \(\in\)AC )

Ta sẽ chứng minh K' \(\equiv\)K 

Thật vậy, gọi giao điểm AC và MN là O ; K'N cắt DC tại I 

dễ thấy O là trung điểm MN

do MN // EI \(\Rightarrow\frac{MO}{EC}=\frac{K'O}{K'C}=\frac{ON}{CI}\)\(\Rightarrow EC=CI\)

\(\Delta NEI\)có NC là đường cao vừa là trung tuyến nên cân tại N

\(\Rightarrow\)NC là đường phân giác của \(\widehat{ENI}\)

Mà \(\widehat{K'NE}+\widehat{ENI}=180^o\) có \(NM\perp NC\)nên NM là  đường phân giác \(\widehat{K'NE}\)( 1 )

mặt khác : NM là đường phân giác \(\widehat{KNE}\) ( 2 )

Từ ( 1 ) và ( 2 ) suy ra \(K'\equiv K\)hay A,K,C thẳng hàng

Answer 2

[Thanh Tùng DZ]

Trên tia đối tia HC lấy D sao cho HD = HC

Tứ giác DECF có DH = HC ; EH = HF nên là hình bình hành

\(\Rightarrow\)DE // CF 

\(\Rightarrow\)DE \(\perp\)CH ; BE \(\perp\)DH

\(\Rightarrow\)E là trực tâm tam giác DBH \(\Rightarrow HE\perp BD\)

Xét \(\Delta DBC\)có DH = HC ; BM = MC nên MH là đường trung bình 

\(\Rightarrow\)MH // BD

\(\Rightarrow\)MH \(\perp EF\)