a + 1 < x < a + 2020
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
3
6 tháng 10 2021
\(1,\Rightarrow2^b\left(2^{a-b}-1\right)=256=2^8\left(a>b\right)\)
Do \(2^b\) chẵn, \(2^{a-b}-1\) lẻ, \(2^8\) chẵn nên \(2^{a-b}-1=1\Leftrightarrow2^{a-b}=2\Leftrightarrow a-b=1\)
\(\Leftrightarrow2^b\cdot1=2^8\Leftrightarrow b=8\Leftrightarrow a=9\)
Vậy \(\left(a;b\right)=\left(8;9\right)\)
12 tháng 7 2021
Bài 1.
Ta có:\(\left(x+\sqrt{x^2+2020}\right)\left(\sqrt{x^2+2020}-x\right)=x^2+2020-x^2=2020\)
\(\Rightarrow\left(x+\sqrt{x^2+2020}\right)\left(y+\sqrt{y^2+2020}\right)=\left(x+\sqrt{x^2+2020}\right)\left(\sqrt{x^2+2020}-x\right)\)
\(\Rightarrow y+\sqrt{y^2+2020}=\sqrt{x^2+2020}-x\)
\(\Rightarrow x+y=\sqrt{x^2+2020}-\sqrt{y^2+2020}\) (1)
Ta có:\(\left(y+\sqrt{y^2+2020}\right)\left(\sqrt{y^2+2020}-y\right)=y^2+2020-y^2=2020\)
\(\Rightarrow\left(x+\sqrt{x^2+2020}\right)\left(y+\sqrt{y^2+2020}\right)=\left(y+\sqrt{y^2+2020}\right)\left(\sqrt{y^2+2020}-y\right)\)
\(\Rightarrow x+\sqrt{x^2+2020}=\sqrt{y^2+2020}-y\)
\(\Rightarrow x+y=\sqrt{y^2+2020}-\sqrt{x^2+2020}\) (2)
Cộng vế với vế của (1) và (2) ta có:
\(2\left(x+y\right)=\sqrt{y^2+2020}-\sqrt{x^2+2020}+\sqrt{x^2+2020}-\sqrt{y^2+2020}\)
\(\Rightarrow2\left(x+y\right)=0\Rightarrow x+y=0\)
12 tháng 7 2021
Bài 2:
Ta có: (2a+1)(2b+1)=9
nên \(2b+1=\dfrac{9}{2a+1}\)
\(\Leftrightarrow2b=\dfrac{9}{2a+1}-\dfrac{2a+1}{2a+1}=\dfrac{8-2a}{2a+1}\)
\(\Leftrightarrow b=\dfrac{8-2a}{4a+2}=\dfrac{4-a}{2a+1}\)
\(\Leftrightarrow b+2=\dfrac{4-a+4a+2}{2a+1}=\dfrac{3a+6}{2a+1}\)
Ta có: \(A=\dfrac{1}{a+2}+\dfrac{1}{b+2}\)
\(=\dfrac{1}{a+2}+\dfrac{2a+1}{3a+6}\)
\(=\dfrac{3+2a+1}{3a+6}\)
\(=\dfrac{2a+4}{3a+6}=\dfrac{2}{3}\)
là:
17 tháng 8 2021
a: Ta có: \(-\left(x+5\right)^2\le0\forall x\)
\(\Leftrightarrow-\left(x+5\right)^2+2021\le2021\forall x\)
Dấu '=' xảy ra khi x=-5
NT
2
TV
0
NA
12 tháng 3 2022
\(a.=\dfrac{2019}{2020}\times\left(\dfrac{4}{11}+\dfrac{5}{11}+\dfrac{2}{11}\right)\\ =\dfrac{2019}{2020}\times1=\dfrac{2019}{2020}\\ b.=\dfrac{25}{27}\times\left(\dfrac{17}{14}-\dfrac{1}{14}-\dfrac{2}{14}\right)\\ =\dfrac{25}{27}\times1=\dfrac{25}{27}\)
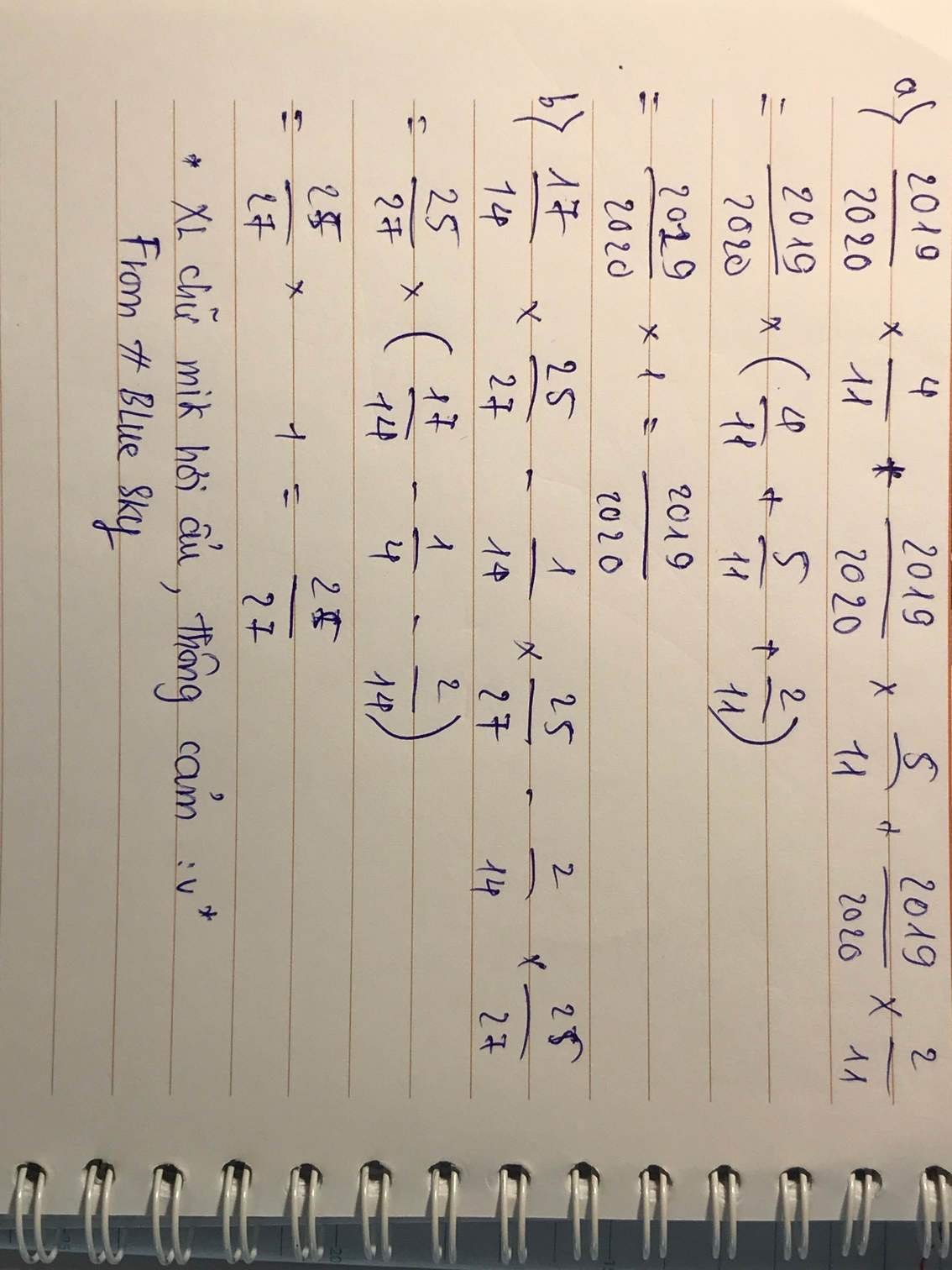
Bạn cho mk hỏi là tìm x có phải tìm a ko?
Nếu ko thì
a + 1 < x < a + 2020
Ta có nếu a = 0 thì
0 + 1 < x < 0 + 2020
1 < x < 2020
\(\Rightarrow\) x \(\in\) {2 ; 2019}
Cứ như vậy ta suy được
Nếu x \(\in\) N (hoặc x \(\in\) Z vì mk ko biết bạn học tập hợp Z chưa)
\(\Rightarrow\) x \(\in\) {a + 1 + 1; a + 1 + 2; ...;a + 1 + 2018}
hoặc x \(\in\) {a + 2020 - 1; a + 2020 - 2;...; a + 2020 - 2018}
hay x \(\in\) {a + 2; a + 3;...; a + 2019}
(mk lấy phần chính ko phải phần "hoặc x \(\in\) {a + 2020 - 1; a + 2020 - 2;...; a + 2020 - 2018}")
Vậy nếu a \(\in\) N thì x \(\in\) {a + 2; a + 3;...; a + 2019}
Chúc bạn học tốt!
a + 1 < x < a + 2020
Ta có nếu a = 0 thì
0 + 1 < x < 0 + 2020
1 < x < 2020
⇒⇒ x ∈∈ {2 ; 2019}
Cứ như vậy ta suy được
Nếu x ∈∈ N (hoặc x ∈∈ Z vì mk ko biết bạn học tập hợp Z chưa)
⇒⇒ x ∈∈ {a + 1 + 1; a + 1 + 2; ...;a + 1 + 2018}
hoặc x ∈∈ {a + 2020 - 1; a + 2020 - 2;...; a + 2020 - 2018}
hay x ∈∈ {a + 2; a + 3;...; a + 2019}
(mk lấy phần chính ko phải phần "hoặc x ∈∈ {a + 2020 - 1; a + 2020 - 2;...; a + 2020 - 2018}")
Vậy nếu a ∈∈ N thì x ∈∈ {a + 2; a + 3;...; a + 2019}