Một chất điểm chuyển động trên một đường tròn bán kính 50 cm. Tốc độ góc của nó có giá trị bằng 2 rad/s. Tính chu kì quay và tốc độ dài của chất điểm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
Hà Đức Thọ
Admin
7 tháng 6 2016
Tốc độ lớn nhất hay nhỏ nhất ứng với quãng đường lớn nhất và nhỏ nhất.
Chu kì dao động của P: \(T=2\pi/\omega=4s\)
\(t=1s=T/4\), trong thời gian này chất điểm M quay một góc là: \(360/4=90^0\)
+ P có quãng đường lớn nhất ứng với chuyển động quanh VTCB, mỗi bên 1 góc \(45^0\), quãng đường: \(S=2.4.\cos 45^0=4\sqrt 2(cm)\)
\(\Rightarrow v = 4\sqrt 2(cm/s)\)
+ P có quãng đường nhỏ nhất ứng với chuyển động quanh biên, mỗi bên 1 góc \(45^0\), quãng đường:
\(S=2.(4-4.\cos45^0)=8-4\sqrt 2(cm)\)
\(\Rightarrow v = 8-4\sqrt 2 cm\)
MH
17 tháng 10 2021
sau 20 s vật quay được 10 vòng
⇒ 1s vật quay được 0,5 vòng
⇒ f = 0,5 vòng/s
ta có \(T=\dfrac{1}{f}=\dfrac{1}{0,5}=2s\)
b, đổi 20cm = 0,2 m
\(T=\dfrac{2\text{π}}{\text{ω}}\)⇒ω\(=\dfrac{2\text{π}}{T}\)\(=\dfrac{2\text{π}}{2}\)\(=\text{π}\) rad/s
\(v=r\text{ω}\)\(=0,2\text{π}\)
c, \(a_{ht}=\dfrac{v^2}{r}=\dfrac{0,4\text{π}^2}{0,2}=0,2\text{π}^2\)
18 tháng 9 2021
a, Ta có : \(T=\dfrac{1}{f}=\dfrac{1}{5}=0,2\left(s\right)\)
b, Ta có : \(C=2\pi r=0,3\pi\left(m\right)\)
\(\Rightarrow v=\dfrac{5C}{1}=\dfrac{5.0,3\pi}{1}=1,5\pi\left(m/s\right)\)
c,Ta có : \(\omega=\dfrac{2\pi}{T}=10\pi\left(rad/s\right)\)
VT
29 tháng 11 2018
Đáp án C
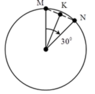
+ Hình chiếu của các điểm M, N và K lên bán kính dao động với chu kì
T = 2 π R v = π 5 s .
+ Hình chiếu của K lên bán kính sẽ dao động với biên độ A = R cos 15 °
Vậy tốc độ trung bình là v t b = 4 A T ≈ 61 , 5 c m / s
VT
13 tháng 5 2018
Đáp án C
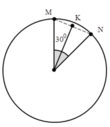
+ Hình chiếu của các điểm M, N và K lên bánh kính dao động với chu kì T = 2 πR v = π 5
→ Hình chiếu của K lên bán kính sẽ dao động với biên độ A = Rcos 15 °
Vậy tốc độ trung bình là v tb = 4 A T ≈ 61 , 5
R=50cm=0,5m
Ta có:T=\(\dfrac{2\pi}{\omega}\)=\(\dfrac{2\pi}{2}\)=\(\pi\)
Ta có:\(\nu\)=r.\(\omega\)=0,5.2=1(m/s)