Mọi người ơi làm ơn giúp mình với ạ, huhu mình cần gấp 😭
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)

IV
1 to have
2 making
3 leaving
4 seeing
5 to get
6 arguing - working
7 to have
8 to seeing
9 not touching
10 to disappoint
V
1 on - on
2 at - at
3 in - in
4 at
5 at
6 in
7 in - in
8 at - in
9 in - at
10 in
VI
1 are - reach
2 comes
3 flies
4 have just decided - will undertake
5 would take
6 was
8 am attending - was attending
9 arrived - was waiting
10 had lived
VII
1 send - will receive
2 will - improve - do
3 will - has
4 doesn't phone - will leave
tờ 2
5 don't study - won't oas
VIII
1 had - would learn
2 told - would be
3 lived - would do
4 would help - knew
5 would buy - had
IX
1 went
2 were
3 wrote
4 could
5 bought
6 studied
7 went
8 would stop
9 were
10 lead
X
1 He opened the window in order to let fresh air in
2 I took my camera so that I could take some phôt
3 He studied really hard in order to get better marks
4 Jason learns Chinese to work in China
5 I've collected money in order that I will buy a new car
XI
1 A new museum has been built in the city center by the council
2The explosion had been caused by a bomb
3 Their flat was broken into last month
4 Jane won't be invited to his birthday party by him


Câu 1.
Tờ vé số có dạng \(\overline{a_1a_2a_3a_4a_5a_6}\in A=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)
\(;a_i\ne a_j\)
Chọn \(a_1\ne0\) nên \(a_1\) có 9 cách chọn.
5 số còn lại là chỉnh hợp chập 5 của 8 số còn lại \(\in A\backslash\left\{a_1\right\}\)
\(\Rightarrow\)Có \(A_8^5\) cách.
Vậy có tất cả \(A_8^5\cdot9=60480\) vé số.

Bài 9:
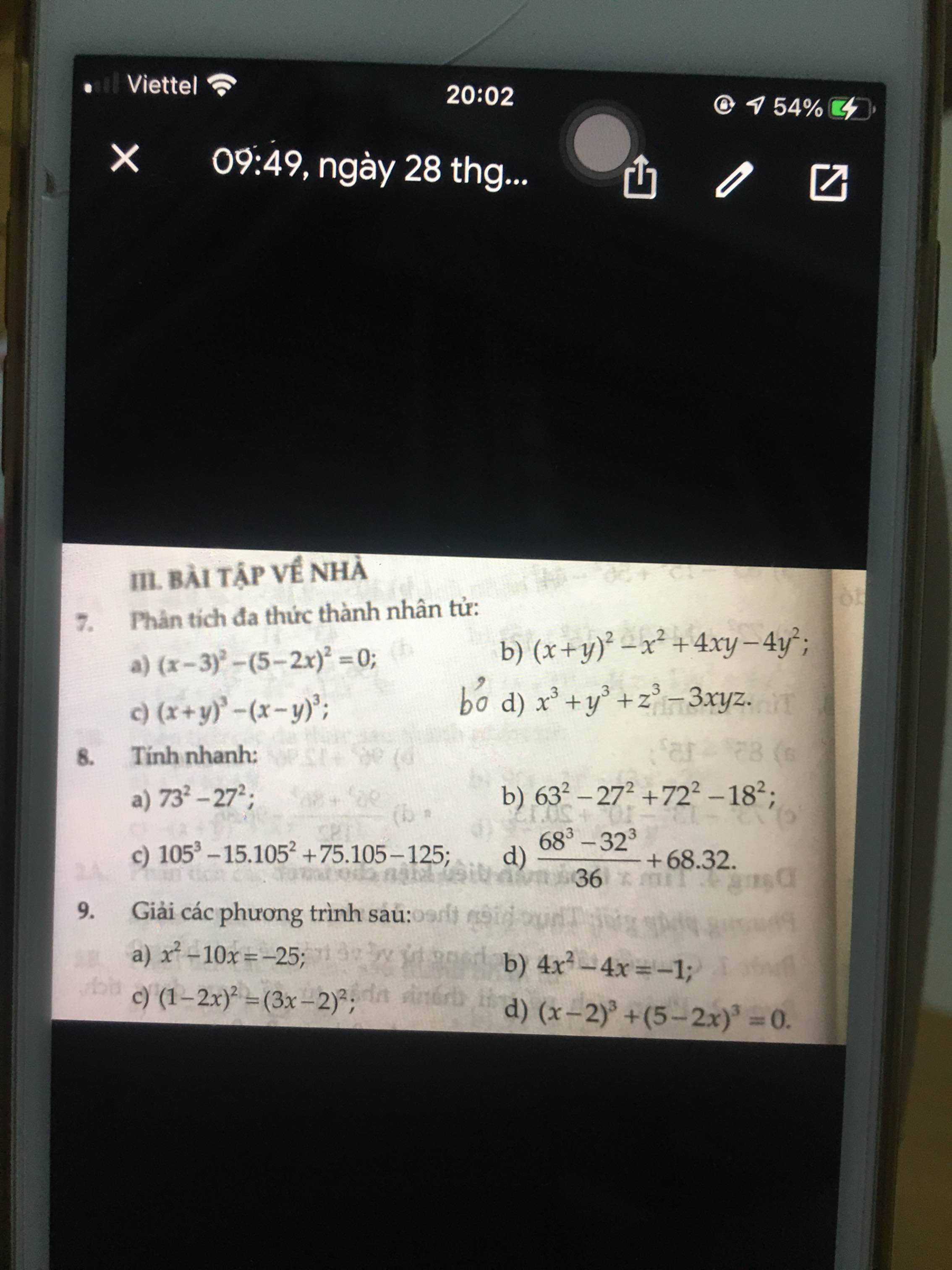
a: Ta có: \(x^2-10x=-25\)
\(\Leftrightarrow x^2-10x+25=0\)
\(\Leftrightarrow x-5=0\)
hay x=5
b: ta có: \(4x^2-4x=-1\)
\(\Leftrightarrow4x^2-4x+1=0\)
\(\Leftrightarrow2x-1=0\)
hay \(x=\dfrac{1}{2}\)
c: Ta có: \(\left(2x-1\right)^2=\left(3x-2\right)^2\)
\(\Leftrightarrow\left(3x-2\right)^2-\left(2x-1\right)^2=0\)
\(\Leftrightarrow\left(3x-2-2x+1\right)\left(3x-2+2x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(5x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{5}\end{matrix}\right.\)

Bài 8:
a: \(73^2-27^2=\left(73-27\right)\left(73+27\right)=4600\)
b: \(63^2-27^2+72^2-18^2\)
\(=\left(63-18\right)\left(63+18\right)+\left(72-27\right)\left(72+27\right)\)
\(=45\cdot\left(63+18+72+27\right)\)
\(=45\cdot180=8100\)


b: Ta có: \(\left(x+y\right)^2-x^2+4xy-4y^2\)
\(=\left(x+y\right)^2-\left(x-2y\right)^2\)
\(=\left(x+y-x+2y\right)\left(x+y+x-2y\right)\)
\(=3y\cdot\left(2x-y\right)\)
c: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=2y^3+6x^2y\)
\(=2y\left(3x^2+y^2\right)\)









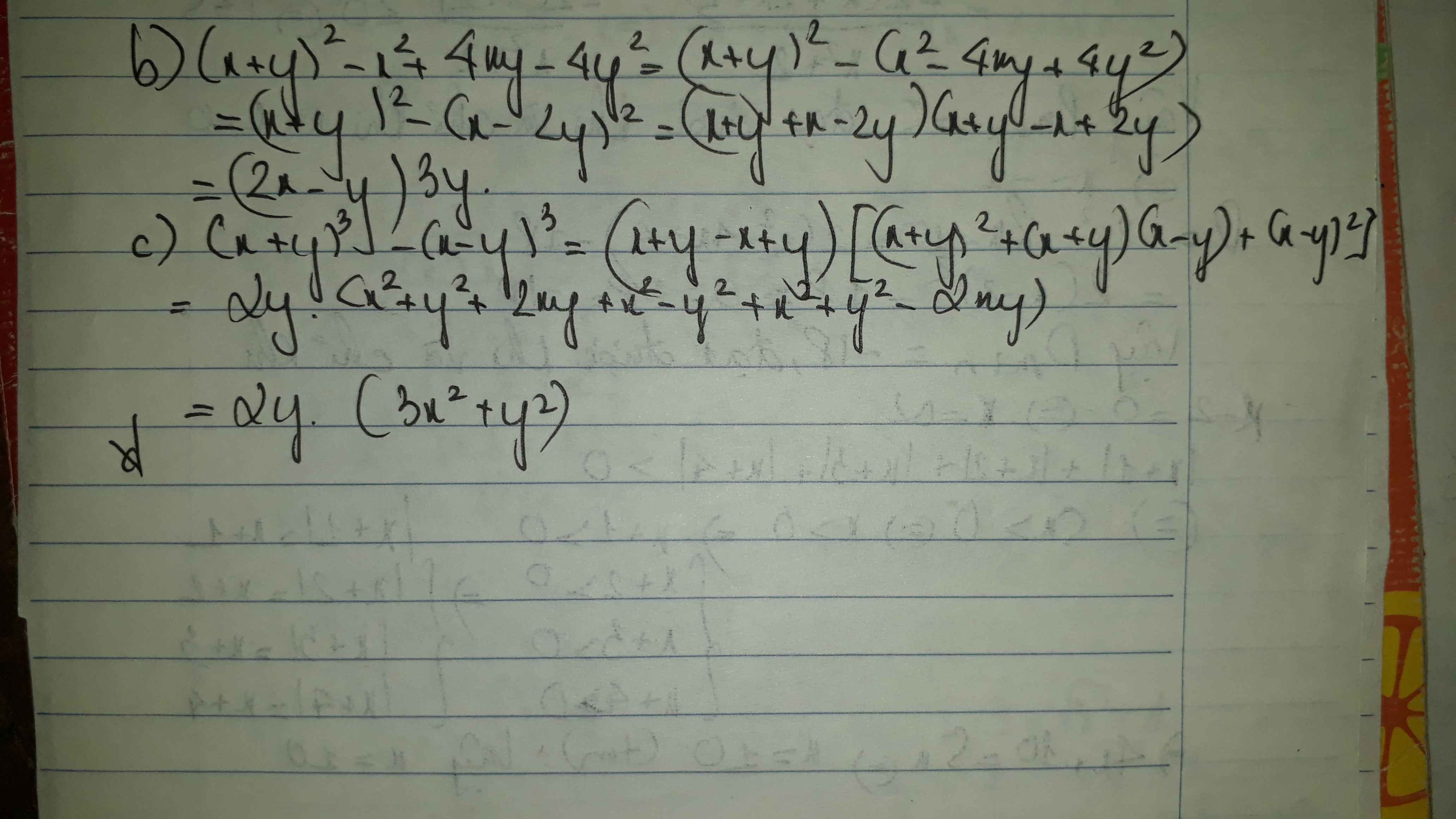

 Mọi người giúp mình với ạ, mình đang gì cần gấp, giúp mình nhé😭😭
Mọi người giúp mình với ạ, mình đang gì cần gấp, giúp mình nhé😭😭