Bài 3: Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH lần lượt tại B', C' và H'.
a) Chứng minh rằng: \(\frac{AH'}{AH}=\frac{B'C'}{BC}\)
Áp dụng: Cho biết \(AH'=\frac{AH}{3}\)và diện tích △ ABC là \(67,5cm^2\). Hãy tính diện tích tam giác AB'C'.
Help me!!! Vẽ cả mình luôn hộ mình...
Đọc tiếp
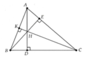
Bài 3: Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH lần lượt tại B', C' và H'.
a) Chứng minh rằng: \(\frac{AH'}{AH}=\frac{B'C'}{BC}\)
Áp dụng: Cho biết \(AH'=\frac{AH}{3}\)và diện tích △ ABC là \(67,5cm^2\). Hãy tính diện tích tam giác AB'C'.
Help me!!! Vẽ cả mình luôn hộ mình nha!
.
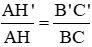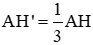và diện tích tam giác ABC là 67,5 cm
Có \(\frac{AH'}{AH}=\frac{B'C'}{BC}=\frac{1}{3}\Rightarrow\frac{\frac{1}{2}.AH'.B'C'}{\frac{1}{2}.AH.BC}=\frac{1}{9}\Leftrightarrow\frac{S_{AB'C'}}{S_{ABC}}=\frac{1}{9}\)
Thây SABC vào tính nhé
Do bài nầy dễ nên nếu có chi tiết thì mình cũng thêm đoạn thẳng song song, hay áp dụng Thales gì đo, rồi dùng t/c bắc cầu sẽ ra đó bạn ơi!