Cho hình chữ nhật ABCD có tâm o cạnh AB = 2a và AD = a. Tính / AB + AD / và / BC - OD /
có ai giúp mình làm bài này với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
4 tháng 9 2021
Lời giải:
1.
$\overrightarrow{2AO}-\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{BC}=\overrightarrow{AB}$
Độ dài: $|\overrightarrow{AB}|=a$
2.
Trên tia đối của $AC$ lấy $T$ sao cho $TA=OC$
Trên tia đối của $BA$ lấy $K$ sao cho $BA=BK$
$\overrightarrow{OC}+2\overrightarrow{AB}=\overrightarrow{TA}+\overrightarrow{AB}+\overrightarrow{AB}$
$=\overrightarrow{TB}+\overrightarrow{AB}$
$=\overrightarrow{TB}+\overrightarrow{BK}=\overrightarrow{TK}$
Ta có:
$TC=3OC=\frac{3}{2}AC=\frac{3}{2}\sqrt{(2a)^2+a^2}=\frac{3\sqrt{5}}{2}a$
$CK=\sqrt{BC^2+BK^2}=\sqrt{(2a)^2+a^2}=\sqrt{5}a$
$\cos \widehat{TCK}=\cos 2\widehat{TCB}=2\cos^2 \widehat{TCB}-1$
$=2(\frac{CB}{AC})^2-1=\frac{3}{5}$
Áp dụng định lý cos:
$TK^2=TC^2+CK^2-2TC.CK\cos \widehat{TCK}$
$=\frac{45}{4}a^2+5a^2-9a^2=\frac{29}{4}a^2$
$\Rightarrow TK=\frac{\sqrt{29}}{2}a$
3. Trên tia đối tia $CD$ lấy $M$ sao cho $CM=CD$
$3\overrightarrow{AB}+2\overrightarrow{OD}=3\overrightarrow{DC}+2\overrightarrow{OD}=2\overrightarrow{OC}+\overrightarrow{DC}$
$=\overrightarrow{AC}+\overrightarrow{DC}=\overrightarrow{AC}+\overrightarrow{CM}=\overrightarrow{AM}$
$AM=\sqrt{AD^2+DM^2}=\sqrt{(2a)^2+(2a)^2}=2\sqrt{2}a$
CM
15 tháng 11 2018
Đáp án C
Gọi O là trung điểm của SD. Ta có: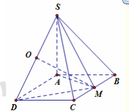
A D = D M = a 2 và A D = 2 a ⇒ A M ⊥ D M
Lại có D M ⊥ S A ⇒ D M ⊥ S A M ⇒ D M ⊥ S M
Vì tam giác SAD vuông tại A nên OS = OD = OA. Tương tự với tam giác SMD nên OS = OD = OM.
Vậy O là tâm mặt cầu ngoại tiếp hình chóp S.ADM. Khi đó R = S D 2 = S A 2 + D A 2 2 = a 6 2 .
\(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=a\sqrt{5}\)
\(\left|\overrightarrow{BC}-\overrightarrow{OD}\right|=\left|\overrightarrow{AD}+\overrightarrow{DO}\right|=AO=\dfrac{a\sqrt{5}}{2}\)