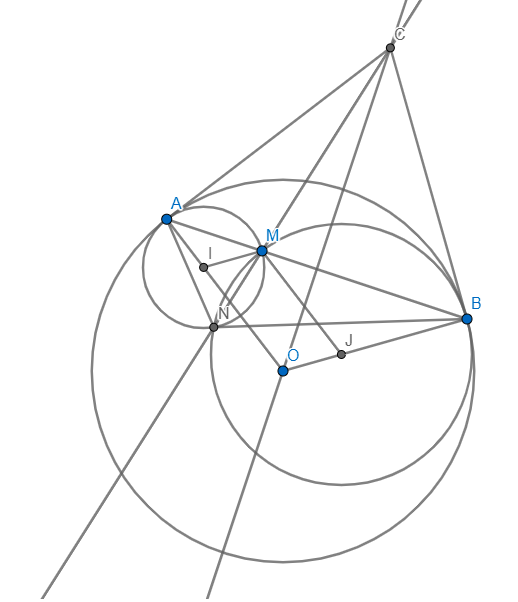
Cho (O) có dây AB cố định.Lấy 1 điểm C bất kì trên đoạn AB.Vẽ đường tròn (P) đi qua C và tiếp xúc với (O) tại A, đường tròn (Q)đi qua C và tiếp xức với (O) tại B. (P) và (Q) cắt nhau tại điểm thiws 2 là M. Tiếp tuyến tại A và B của (O) cắt nhau tại I
a)Chứng minh MC lf phân giác AMB
b)Gọi giao của OM và AB là K.Chứng minh AC/AB=AK/BK
c)Chuwnngs minh rằng khi C thay đổi từ tâm đường tròn ngoại tiếp tam giác MPQ luôn thuộc 1 đường thẳng cố định