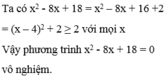: Chứng tỏ rằng phương trình: lxl + 1 = 0 vô nghiệm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
15 tháng 8 2018
Ta có: 2(1 – 1,5x) + 3x = 0 ⇔ 2 – 3x + 3x = 0 ⇔ 2 + 0x = 0
Vậy phương trình vô nghiệm.
PT
1
PT
1
CM
28 tháng 3 2017
Ta có: 2(x + 1) = 3 + 2x ⇔ 2x + 2 = 3 + 2x ⇔ 0x = 1
Vậy phương trình vô nghiệm.
PT
1
BV
3
18 tháng 4 2018
\(a)\) Ta có :
\(\left(x-1\right)^2\ge0\)
\(3x^2\ge0\)
\(\Rightarrow\)\(\left(x-1\right)^2+3x^2\ge0\)
Dấu "=" xảy ra tức là phương trình có nghiệm x khi và chỉ khi \(\hept{\begin{cases}\left(x-1\right)^2=0\\3x^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x-1=0\\x^2=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=1\\x=0\end{cases}}}\)
Vậy phương trình có nghiệm \(x=0\) và \(x=1\)
Đề sai nhé
18 tháng 4 2018
\(b)\) Ta có :
\(x^2+2x+3\)
\(=\)\(\left(x^2+2x+1\right)+2\)
\(=\)\(\left(x+1\right)^2+2\ge2>0\)
Vậy đa thức \(x^2+2x+3\) vô nghiệm
Em mới lớp 7 có gì sai anh thông cảm nhé
DC
2
12 tháng 2 2020
a) Ta có: \(x^2+2x+3\)
\(=\left(x^2+2x+1\right)+2\)
\(=\left(x+1\right)^2+2>0\)
Vậy pt vô nghiệm
12 tháng 2 2020
b) Ta có \(x^2+2x+4\)
\(=\left(x^2+2x+1\right)+3\)
\(=\left(x+1\right)^2+3>0\)
Vậy pt vô nghiệm
CM
25 tháng 11 2019
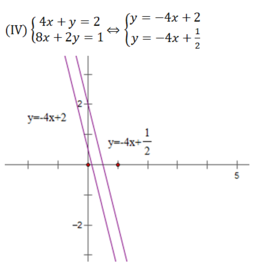
Hai đường thẳng trên song song nên chúng không có điểm chung hay hệ phương trình (IV) vô nghiệm.
Phương pháp thế:
Ta có ( biểu diễn y theo x từ phương trình thứ nhất):
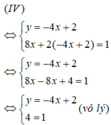
Vậy hệ phương trình (IV) vô nghiệm.
NT
1
