1) Trên mp tọa độ Oxy, cho đường thẳng y=(2m+1)x-4m-1 và điểm A(-2;3). Tìm m để khoảng cách từ A đến đường thẳng trên là lớn nhất.
2) Trên mp tọa độ Oxy, cho A(2;3) và điểm B(1;-4) và điểm C nằm trên trục Ox. Tìm tọa độ điểm C để tam giác ABC có chu vi nhỏ nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2mx -4m +10x -1 -y =0
2m(x-2) +(10x -1-y) =0
x =2 ; y =19 pt đúng với mọi m
=> h/s luôn qua điểm M(2;19) gọi K/c từ A đến d là AH
khoảng cách lờn nhất AH= AM ( AH </ AM)
khi đó AH vuông góc AM
+ gọi pt qua AM là y =ax +b => a =4 ; b =11
=>(2m+10) . 4 =-1
2m = -1/4 -10 =- 41/4
m =-41/8

1: Để hai đường thẳng cắt nhau thì
2m+1<>m+2
hay m<>1

b: Phương trình hoành độ giao điểm là:
\(\dfrac{-1}{2}x^2-4x+16=0\)
\(\Leftrightarrow x^2\cdot\dfrac{1}{2}+4x-16=0\)
\(\Leftrightarrow x^2+8x-32=0\)
\(\Leftrightarrow\left(x+4\right)^2=48\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\sqrt{3}-4\\x=-4\sqrt{3}-4\end{matrix}\right.\)
Khi \(x=4\sqrt{3}-4\) thì \(y=\dfrac{-1}{2}\cdot\left(4\sqrt{3}-4\right)^2=-32+16\sqrt{3}\)
Khi \(x=-4\sqrt{3}-4\) thì \(y=\dfrac{-1}{2}\left(-4\sqrt{3}-4\right)^2=-32-16\sqrt{3}\)
b: Để hai đường song song thì
\(\left\{{}\begin{matrix}m-1=-1\\m+3< >1\end{matrix}\right.\Leftrightarrow m=0\)

Để đường thẳng (d) đi qua điểm A(1, -5), ta cần giải hệ phương trình sau:
y = (2m + 3)x - (m^2 + 3m + 2) (1)
y = x^2 (2)
Thay x = 1 vào (1), ta có:
y = 2m + 3 - (m^2 + 3m + 2)
y = -m^2 - m + 1
Thay y từ (2) vào biểu thức trên, ta có:
x^2 = -m^2 - m + 1
x^2 + m^2 + m - 1 = 0
Để đường thẳng (d) đi qua điểm A(1, -5), phương trình (1) phải có nghiệm là y = -5 khi x = 1. Thay x = 1 và y = -5 vào (1), ta có:
-5 = 2m + 3 - (m^2 + 3m + 2)
m^2 + m - 10 = 0
(m + 2)(m - 5) = 0
Vậy, m = -2 hoặc m = 5.
Khi đó, phương trình của đường thẳng (d) sẽ là:
Khi m = -2: y = -x^2 - x - 1Khi m = 5: y = 13x - 24Thay x=1 và y=-5 vào (d), ta được:
2m+3-m^2-3m-2=-5
=>-m^2-m+6=0
=>m^2+m-6=0
=>(m+3)(m-2)=0
=>m=2 hoặc m=-3

Gọi pt BC có dạng: \(y=ax+b\Rightarrow\left\{{}\begin{matrix}0=6a+b\\3=a.0+b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=3\\a=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow y=-\dfrac{1}{2}x+3\)
Pt hoành độ giao điểm BC và d:
\(-\dfrac{1}{2}x+3=mx-2m+2\)
\(\Leftrightarrow m\left(x-2\right)+\dfrac{1}{2}\left(x-2\right)=0\)
\(\Leftrightarrow\left(m+\dfrac{1}{2}\right)\left(x-2\right)=0\Rightarrow x=2\Rightarrow y=2\)
Vậy \(d_m\) luôn cắt BC tại điểm A cố định có tọa độ \(A\left(2;2\right)\)
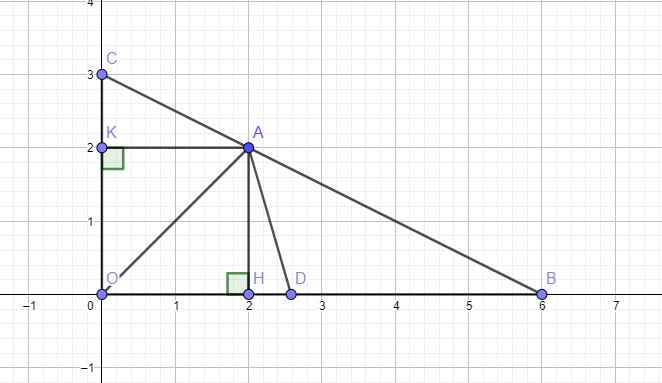
b. Ta có: \(OB=\left|x_B\right|=6;OC=\left|y_C\right|=3\)
Từ A kẻ AH vuông góc trục hoành và AK vuông góc trục tung
\(\Rightarrow AH=\left|y_A\right|=2\) ; \(AK=\left|x_A\right|=2\)
\(S_{OAC}=\dfrac{1}{2}AK.OC=\dfrac{1}{2}.2.3=3\) ; \(S_{OAB}=\dfrac{1}{2}AH.OB=6\)
\(S_{OBC}=\dfrac{1}{2}OB.OC=9\)
Giả sử \(d_m\) cắt cạnh OC tại 1 điểm D nằm giữa O và C
\(\Rightarrow S_{ACD}=S_{OAC}-S_{OAD}< S_{OAC}=3< \dfrac{1}{2}S_{OBC}=9\) (ktm)
\(\Rightarrow d_m\) phải cắt cạnh OB tại 1 điểm D nào đó nằm giữa O và B
Khi đó: \(S_{ABD}=\dfrac{1}{2}S_{OBC}=\dfrac{9}{2}\)
Mà \(S_{ABD}=\dfrac{1}{2}AH.BD\Rightarrow BD=\dfrac{2S_{ABD}}{AH}=\dfrac{9}{2}\)
\(\Rightarrow x_B-x_D=\dfrac{9}{2}\Rightarrow x_D=6-\dfrac{9}{2}=\dfrac{3}{2}\)
\(\Rightarrow D\left(\dfrac{3}{2};0\right)\)
Do \(d_m\) qua D nên: \(\dfrac{3}{2}m-2m+2=0\Rightarrow m=4\)