Tìm giá trị nhỏ nhất của đa thức \(g\left(x\right)=16x^4-72x^2+90\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



do 16x4 \(\ge\)0
72x2 \(\ge\)0
=> 16x^4 - 72x^2 \(\ge\)0
=> 16x^4 - 72x^2 + 90 \(\ge\)0
hay G(x) \(\ge\)90
GTNN của G(x) = 90
dấu = xảy ra <=> x = 0

a) Giải:
\(f\left(x\right)=\left(m^2-25\right)x^4+\left(20+4\right)x^3+7x^2-9\) là đa thức bậc \(3\) theo biến \(x\) khi:
\(\left\{{}\begin{matrix}m^2-25=0\\20+4m\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=\pm5\\m\ne-5\end{matrix}\right.\)
Vậy \(m=5\) thì \(f\left(x\right)\) là đa thức bậc \(3\) theo biến \(x\)
b) Ta có:
\(g\left(x\right)=16x^4-72x^2+90\)
\(=\left(4x^2\right)^2-2.4x^2.9+9^2+9\)
\(=\left(4x^2-9\right)^2+9\)
Với mọi giá trị của \(x\) ta có: \(\left(4x^2-9\right)^2\ge0\)
\(\Rightarrow g\left(x\right)=\left(4x^2-9\right)^2+9\ge9\)
Dấu "=" xảy ra khi \(\Leftrightarrow\left(4x^2-9\right)^2=0\Leftrightarrow x=\pm\dfrac{3}{2}\)
Vậy GTNN của đa thức \(g\left(x\right)\) là \(9\) tại \(x=\pm\dfrac{3}{2}\)

Xét hàm số f(x) = x 3 + 3 x 2 − 72x + 90 trên đoạn [-5;5]
f′(x) =3 x 2 + 6x − 72;
f′(x) = 0 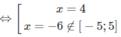
f(−5) = 400; f(5) = −70; f(4) = −86
Ngoài ra, f(x) liên tục trên đoạn [-5;5] và f(−5).f(5) < 0 nên tồn tại x 0 ∈ (−5;5) sao cho f( x 0 ) = 0
Ta có g(x) = |f(x)| ≤ 0 và g( x 0 ) = |f( x 0 )| = 0;
g(−5) = |400| = 400
g(5) = |−70| = 70; g(4) = |f(4)| = |−86| = 86
Vậy min g(x) = g( x 0 ) = 0; max g(x) = g(−5) = 400

+) \(E=x^2-6x+9+x^2-22x+121=2x^2-28x+130\)
\(\Rightarrow2E=4x^2-56x+242=\left(4x^2-56x+196\right)+46=\left(2x-14\right)^2+46\)
Vì \(\left(2x-14\right)^2\ge0\Rightarrow2E=\left(2x-14\right)^2+46\ge46\Rightarrow E\ge23\)
Dấu "=" xảy ra khi x=7
Vậy Emin=23 khi x=7
+) \(F=\frac{-2}{x^2-2x+5}=\frac{-2}{x^2-2x+1+4}=\frac{-2}{\left(x-1\right)^2+4}\)
Vì \(\left(x-1\right)^2\ge0\Rightarrow\left(x-1\right)^2+4\ge4\Rightarrow F=\frac{-2}{\left(x-1\right)^2+4}\le-\frac{2}{4}=-\frac{1}{2}\)
Dấu "=" xảy ra khi x=1
Vậy Fmin=-1/2 khi x=1
+) \(G=\left(x+1\right)\left(x-2\right)\left(x-3\right)\left(x-6\right)=\left(x^2-6x+x-6\right)\left(x^2-3x-2x+6\right)=\left(x^2-5x-6\right)\left(x^2-5x+6\right)\)
Đặt x2-5x=t, ta được:
\(G=\left(t-6\right)\left(t+6\right)=t^2-36=\left(x^2-5x\right)^2-36\)
Vì \(\left(x^2-5x\right)^2\ge0\Rightarrow G=\left(x^2-5x\right)^2-36\ge36\)
Dấu "=" xảy ra khi x=0 hoặc x=5
Vậy Gmin=36 khi x=0 hoặc x=5

TK: Tìm Min (x^4 + 1) (y^4 + 1) với x + y = căn10 ; x , y > 0 - Thanh Truc
Tìm giá trị nhỏ nhất của đa thức g(x)=16x4-72x2+90
Ta có:
g(x)=16x4−72x2+90
=(4x2)2−2.4x2.9+92+9
=(4x2−9)2+9
Với mọi giá trị của x ta có: (4x2−9)2≥0
⇒g(x)=(4x2−9)2+9≥9
Dấu "=" xảy ra khi ⇔(4x2-9)2=0⇔x=± \(\frac{3}{2}\)
Vậy GTNN của đa thức \(g\left(x\right)\)là 9 tại x=\(\pm\frac{3}{2}\)
4x2 nghĩa là4x2nha mấy cái khác cũng v