Một lớp có 32 học sinh xếp hành thành 2 hình vuông lồng vào nhau một trong một ngoài.Hỏi cần bao nhiêu học sinh để xếp thành 3 hình vuông như thế theo hướng cạnh mỗi hình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 9 2019
Chọn A
Gọi A là biến cố: Xếp hai học sinh A, B ngồi ở hai bàn xếp cạnh nhau.
Số cách xếp ngẫu nhiên học sinh vào 36 cái bàn là 36!, 
Ta tìm số cách xếp thuận lợi cho biến cố :
- Chọn 1 hàng hoặc 1 cột có C 12 1 cách;
- Mỗi hàng hoặc cột đều có 6 bàn nên có 5 cặp bàn xếp kề nhau, chọn lấy 1 trong 5 cặp bàn cạnh nhau trong hàng hoặc cột vừa chọn ra có C 5 1 cách;
- Xếp A và B vào cặp bàn vừa chọn có 2! cách;
- Xếp 34 học sinh còn lại có 34! cách.
Vậy tổng số cách xếp thoả mãn là: 
Vậy xác suất cần tính: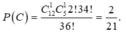 
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
31 tháng 3 2023
Độ dài mỗi cạnh của bàn hình vuông đủ để cho số học sinh ngồi là:
8:4=2(học sinh)
Nếu xếp 9 bàn cạnh nhau thành hàng bàn hình chữ nhật, chiều rộng có độ dài 1 cạnh hình vuông, chiều dài có độ dài 9 lần cạnh bàn hình vuông.
Số học sinh của lớp:
2 x (9 + 1 + 9 + 1)= 40 (học sinh)
KZ
26 tháng 10 2021
Số hàng dọc nhiều nhất có thể xếp đc bằng ƯCLN (42; 48; 54)
Ta có:
42= 2.3.7
48= 24.3
54= 2.33
\(\Rightarrow\)ƯCLN (42; 48; 54)= 2.3= 6
Vậy số hàng dọc xếp đc nhiều nhất là 6 hàng
Khi đó mỗi hàng có số hs là:
6A: 54 : 6= 9 (hs)
6B: 42 : 6 = 7 (hs)
6C: 48 : 6 = 8 (hs)
#miu
#armybts
LT
22 tháng 11 2021
Số hàng dọc = ƯCLN (300 ; 276 ; 252) = 12
K6 có 300 : 12 = 25
K7 có 276: 12 = 23
K8 có 252 : 12 = 21
NL
22 tháng 11 2021
Gọi số hàng dọc có thể xếp được nhiều nhất là aa (hàng, a∈Na∈ℕ*, aa lớn nhất).
⇒300⋮a⇒300⋮a ; 276⋮a276⋮a ; 252⋮a252⋮a
Mà a∈Na∈ℕ*, aa lớn nhất
nên a∈ƯCLN(300,276,252)a∈ƯCLN(300,276,252)
Ta có: ⎧⎪⎨⎪⎩300=22.3.52276=22.3.23252=22.32.7{300=22.3.52276=22.3.23252=22.32.7
⇒ƯCLN(300,276,252)=22.3=4.3=12⇒ƯCLN(300,276,252)=22.3=4.3=12
⇒a=12⇒a=12
Như vậy, có thể xếp được nhiều nhất 1212 hàng dọc.
Khi đó, khối 66 có: 300:12=25300:12=25 (hàng)
khối 77 có: 276:12=23276:12=23 (hàng)
khối 88 có: 252:12=21252:12=21 (hàng)
