Tìm phân số \(\frac{a}{b}\)bằng \(\frac{14}{21}\)và UCLN(a,b)=19
_Thanks mn_
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
16 tháng 6 2021
Ta có: 
là phân số tối giản
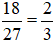
Vậy phân số tối giản của phân số 
Mà ƯCLN(a ; b) = 13 nên ta có: 
a : 13 = 2 ⇒ a = 26.
b : 13 = 3 ⇒ b = 39.
Vậy phân số cần tìm là 
16 tháng 6 2021
Ta có: 18/27=2/3 là phân số tối giản.
Vậy phân số tối giản của phân số a/b=2/3
Mà ƯCLN(a ; b) = 13 nên ta có: a/b=a:13/b:13=2/3
a : 13 = 2 ⇒ a = 26.
b : 13 = 3 ⇒ b = 39.
Vậy phân số cần tìm là 26/39
10 tháng 7 2017
Dù đăng cách đây lâu rồi nhưng vẫn thích làm bài anh Tú đăng :P
Theo đề bài ta có:
\(\dfrac{a}{b}_{MIN}\)
\(\Rightarrow a_{MIN};b_{MAX}\)
\(\dfrac{a}{b}:\dfrac{9}{14}=N\Rightarrow\dfrac{a}{b}.\dfrac{14}{9}=N\Rightarrow a\in B\left(9\right);b\inƯ\left(14\right)\)
\(\dfrac{a}{b}:\dfrac{21}{35}=N\Rightarrow\dfrac{a}{b}.\dfrac{35}{21}=N\Rightarrow a\in B\left(21\right);b\inƯ\left(35\right)\)
\(a_{MIN}\Rightarrow a\in BCNN\left(9;21\right)\Rightarrow a=63\)
\(b_{MAX}\Rightarrow b\in UCLN\left(14;35\right)\Rightarrow b=7\)\(\)
Phân số cần tìm là \(\dfrac{63}{7}\)
