Cho tam giác ABC có cạnh BC = m. Trên cạnh AB lấy các điểm D, E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC cắt cạnh AC theo thứ tự ở M và N. Tính độ dài các đoạn thẳng DM, EN theo m
giải nhanh giúp mình với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LV
11 tháng 2 2020
Dựa vào tính chất đường trung bình của tam giác:
DM=EN/2
theo tính chất đương trung bình của hình thang:
EN=(DM+m)/2
CM
6 tháng 2 2018
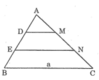
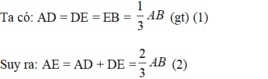
Trong ΔABC, ta có: DM // BC (gt)
Nên 
(Hệ quả định lí Ta-lét)
Suy ra : 
(3)
Từ (1) và (3) suy ra: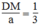 
Suy ra: 
Trong ΔABC, ta có: EN // BC (gt)
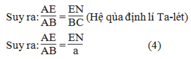
Từ (2) và (4) suy ra: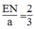 
hay 
6 tháng 12 2016
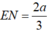
qua N kẻ đường thẳng song song với AB cắt BC tại K .
Vì EN song song với BK; NK song song với EB nên EB=NK;EN=BK (tính chất đoạn chắn)
nên NK=AD. Vì DM song song với BC nên góc( từ sau góc mình kí hiệu là >) DMA = >ACB . Vì NK song song với AB nên >A= >KNC \(\Rightarrow\) >B=>NKC Do đó ΔADM=ΔNKC (g.c.g). nên DM=KC
Suy ra DM+EN=BK+CK=BC(dpcm)
CM
3 tháng 5 2019
Từ N kẻ đường thẳng song song vói AB cắt BC tại K. Nối EK.
Xét ΔBEK và Δ NKE, ta có:
∠(EKB) =∠(KEN) (so le trong vì EN // BC)
EK cạnh chung
∠(BEK) =∠(NKE) (so le trong vì NK // AB))
Suy ra: Δ BEK = Δ NKE(g.c.g)
Suy ra: BE = NK (hai cạnh tương ứng)
EN = BK (hai cạnh tương ứng)
Xét Δ ADM và Δ NKC, ta có:
∠A =∠(KNC) (đồng vị vì NK // AB)
AD = NK ( vì cùng bằng BE)
∠(ADM) =∠(NKC) (vì cùng bằng góc B)
Suy ra: Δ ADM = Δ NKC(g.c.g)
Suy ra: DM = KC (hai cạnh tương ứng)
Mà BC = BK + KC. Suy ra: BC = EN + DM
28 tháng 12 2017
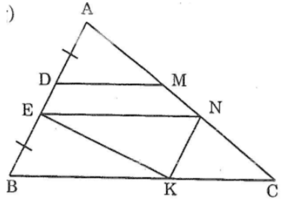
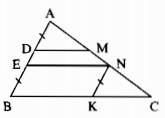
Từ N kẻ đường thẳng song song với AB cắt BC tại K. Nối EK.
Xét ∆BEK và ∆NKE, ta có:
ˆEKB=ˆKENEKB^=KEN^ (so le trong vì EN // BC)
EK cạnh chung
ˆBEK=ˆNKEBEK^=NKE^ (so le trong vì NK // AB)
Suy ra: ∆BEK = ∆NKE (g.c.g)
Suy ra: BE = NK (hai cạnh tương ứng)
EN = BK (hai cạnh tương ứng)
Xét ∆ADM và ∆NKC, ta có:
ˆA=ˆKNCA^=KNC^ (đồng vị vì NK // AB)
AD = NK (vì cùng bằng BE)
ˆADM=ˆNKCADM^=NKC^ (vì cùng bằng ˆBB^)
Suy ra: ∆ADM = ∆NKC (c.g.c)
=>DM = KC (hai cạnh tương ứng)
Mà BC = BK + KC. Suy ra: BC = EN + DM
HH
15 tháng 4 2020
Kẻ NF // AB (F thuộc BC)
Xét tam giác BEF và tam giác NFE có:
BEF = NFE (2 góc so le trong, NF // BE)
FE chung
EFB = FEN (2 góc so le trong, EN // FB)
=> Tam giác BEF = Tam giác NFE (g.c.g)
=> BE = NF (2 cạnh tương ứng)
mà BE = AD (gt)
=> AD = NF
Xét tam giác ADM và tam giác NFC có:
MDA = CFN (2 góc đồng vị, DM // FC)
DA = FN (chứng minh trên)
DAM = FNC (2 góc đồng vị, AD // NF)
=> Tam giác ADM = Tam giác NFC (g.c.g)
=> DM = FC (2 cạnh tương ứng)
mà EN = BF (tam giác BEF = tam giác NFE)
=> DM + EN = BF + FC = BC
