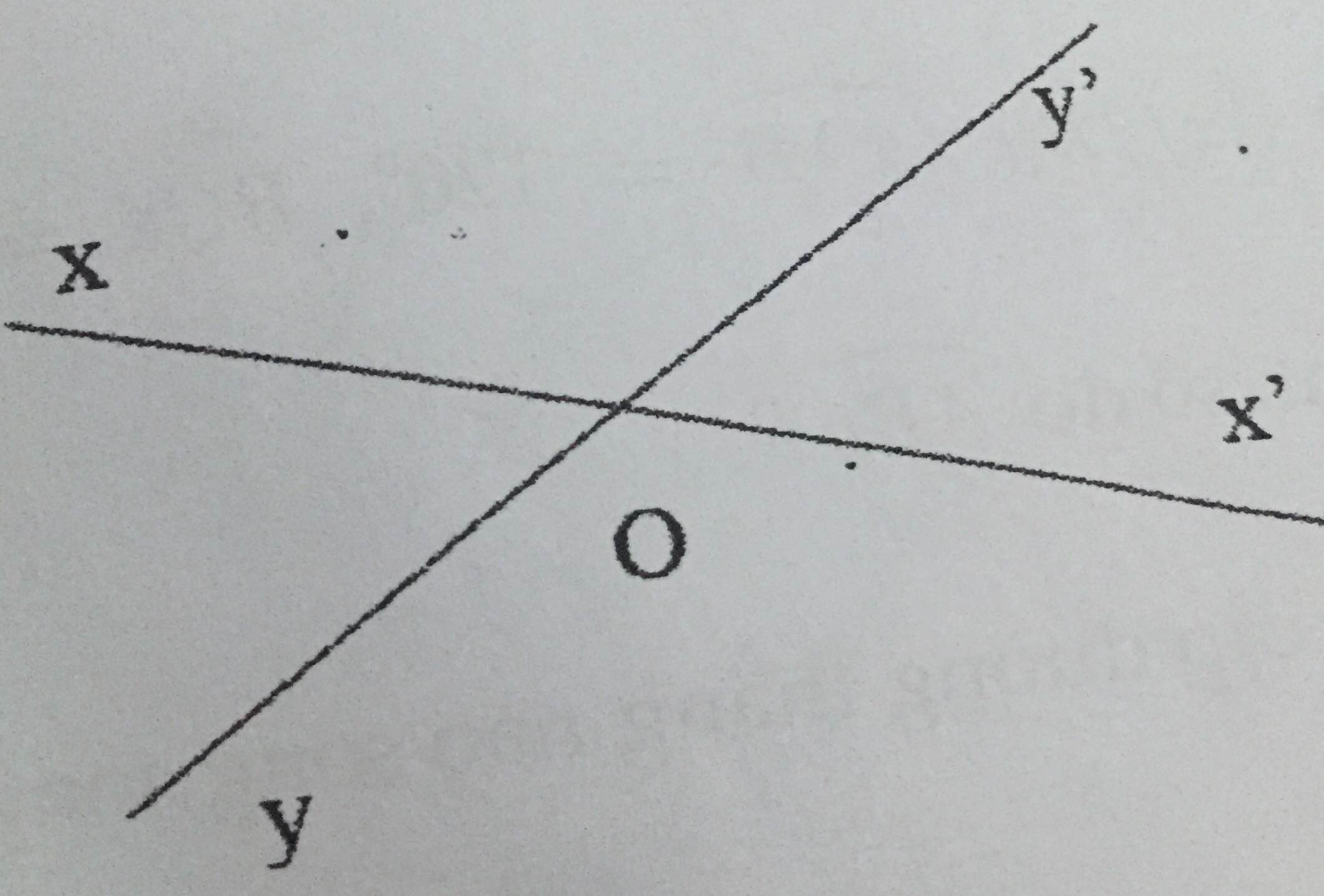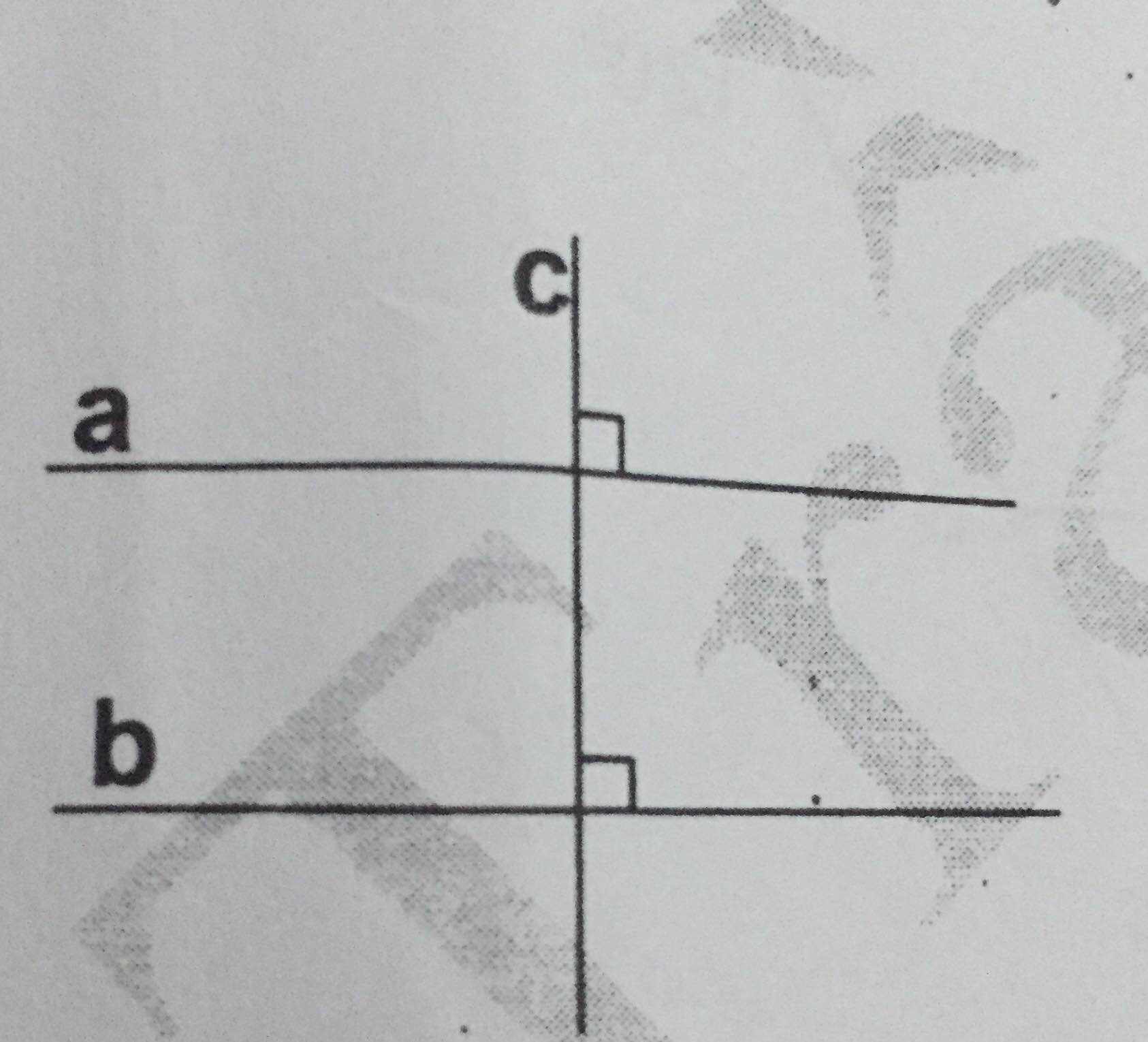ghi giả thiết và kết luận của định lí minh hoạ bởi cách hình vẽ sau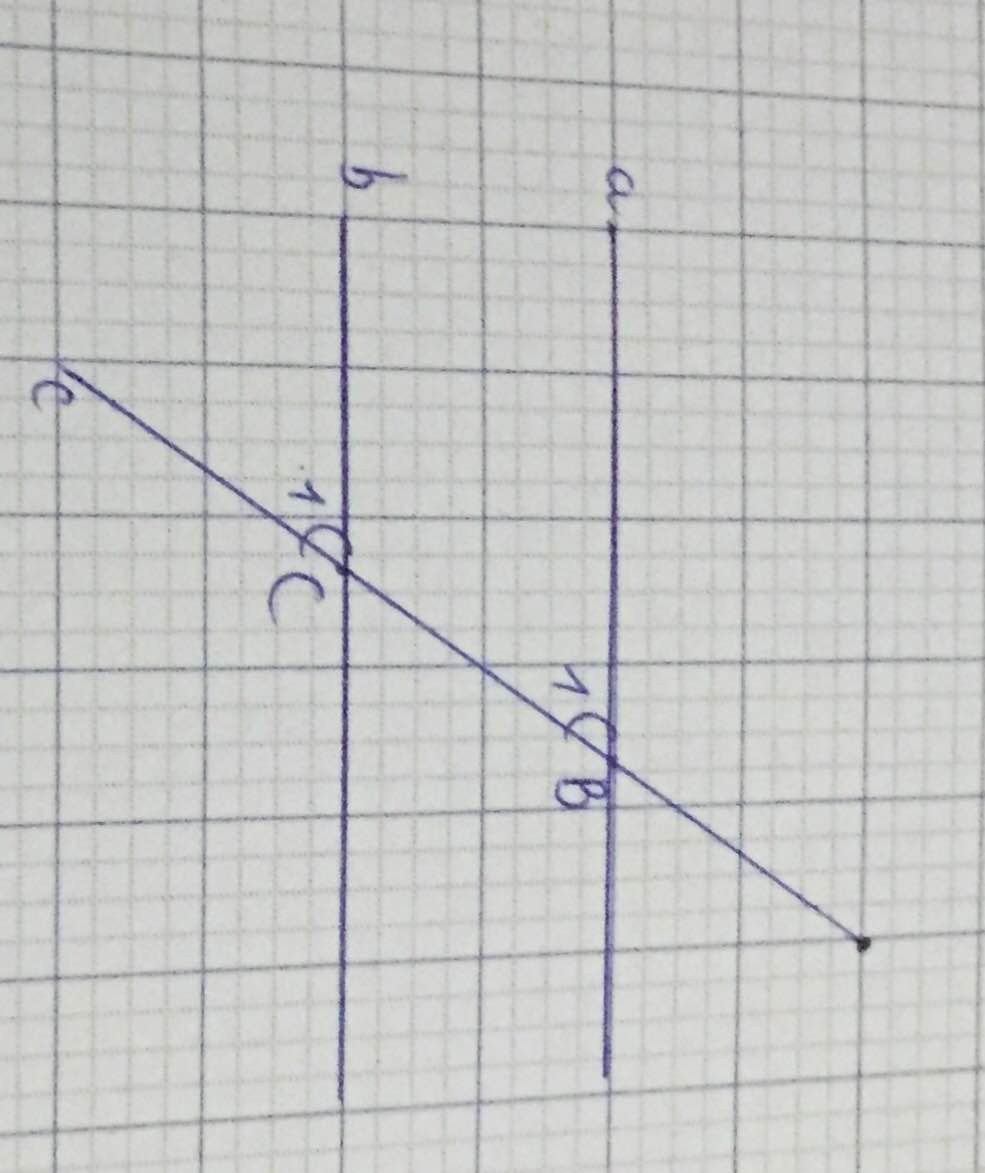
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
1
NH
Nguyễn Hoàng Minh
18 tháng 10 2021
| GT | a//b |
| KL | \(\widehat{C_1}=\widehat{B_1}\) (2 góc đồng vị) |
Đúng(1)
Những câu hỏi liên quan
NL
1
18 tháng 10 2021
| GT | Ox đối Ox' ; Oy đối Oy' |
| KL | \(\widehat{xOy}=\widehat{x'Oy'};\widehat{xOy'}=\widehat{x'Oy}\) (các cặp góc đối đỉnh |
NL
1
PT
1
CM
6 tháng 4 2018
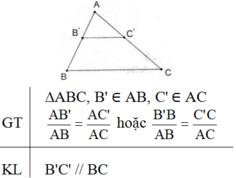
Định lí Talet đảo:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
IM
3 tháng 10 2016
| Giả thiết | Góc O1 và góc O3 đối đỉnh |
| Kết luận | Góc O1 = Góc O3 |
C/m :
Ta có :
\(\begin{cases}\widehat{O_1}+\widehat{O_2}=180^0\\\widehat{O_3}+\widehat{O_2}=180^0\end{cases}\) ( kề bù )
\(\Rightarrow\begin{cases}\widehat{O_1}=180^0-\widehat{O_2}\\\widehat{O_3}=180^0-\widehat{O_2}\end{cases}\)
\(\Rightarrow\widehat{O_1}=\widehat{O_3}\left(đpcm\right)\)
PT
1
CM
17 tháng 4 2018
Hình minh họa và viết giả thiết kết luận bằng kí hiệu:
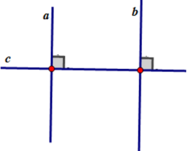
Giả thiết: a⊥c, b⊥c
Kết luận: a//b
AQ
4
3 tháng 8 2015
Vì góc O1 và góc O2 kề bù => O1 + O2 = 180o
Góc góc O2 và góc O3 kề bù => O2 + O3 = 180o
=> O1 = O2
