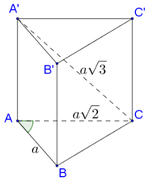
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông cân tại A, BC=2CC'.Gọi I,K lần lượt là trung điểm của BC và A'I. Chứng minh:
a) B'C' vuông góc (A'AI).
b) AK vuông góc (A'BC).
c, Gọi K là hình chiếu vuông góc của A trên AC. CM: B,H,K thẳng hàng
Ai cố giúp mình cả 3 câu vs, đề khó wa:)))

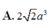
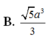
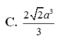
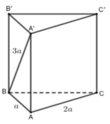
a) Ta có:
\(AA'\perp\left(ABC\right)\Rightarrow BC\perp AA'\left(1\right)\)
\(\Delta ABC\) vuông cân tại $A$, $I$ là trung điểm $BC$ \(\Rightarrow BC\perp AI\left(2\right)\)
Từ $(1)$ và $(2)$ suy ra: \(BC\perp\left(A'AI\right)\) mà \(B'C'//BC\Rightarrow B'C'\perp\left(A'AI\right)\)
b) Ta có $\Delta ABC$ vuông cân tại $A$
$\Rightarrow AI = \dfrac{1}{2}BC=CC'=A'A$
$\Rightarrow \Delta A'AI$ cân tại $A$ mà $K$ là trung điểm $AI$ $\Rightarrow$ \(AK\perp A'I\left(3\right)\)
Lại có \(BC\perp\left(A'AI\right)\) mà \(AK\subset\left(A'AI\right)\Rightarrow AK\perp BC\left(4\right)\)
Từ $(3)$ và $(4)$ suy ra: \(AK\perp\left(A'BC\right)\)
c) Ta có \(AK\perp\left(A'BC\right)\Rightarrow AK\perp A'C\left(5\right)\)
Lại có \(AB\perp AC\) và \(AB\perp AA'\Rightarrow AB\perp\left(A'AC\right)\Rightarrow AB\perp A'C\left(6\right)\)
Theo giả thiết \(AH\perp A'C\left(7\right)\)
Từ $(5), (6)$ và $(7)$ suy ra $AH,AK, AB$ cùng nằm trong mặt phẳng \(\left(\alpha\right)\) vuông góc với $A'C$
\(\Rightarrow H,K,B\) cùng thuộc \(\left(\alpha\right)\) mà $H,K,B$ cùng thuộc $(A'BC)$
\(\Rightarrow H,K,B\) thuộc giao tuyến của \(\left(\alpha\right)\) với $(A'BC)$
\(\Rightarrow B,H,K\) thẳng hàng
Hình minh họa thôi nhé !!